AMP と Autocast
AMP(Automatic Mixed Precision)とは、モデルの計算をFP32(単精度)とFP16(半精度)で切り替えて実行する技術。これにより訓練速度向上やGPUメモリ使用量削減が期待できます。Autocast 機能は、この技術を簡単に実装できるように設計されています。この記事では AMP の基本と autocast 機能の使い方について解説します。また、GradScaler を使用することで、精度の低下を回避できます。
読み込みが遅い場合はキャッシュを有効にしてください。ブラウザはデフォルトで有効になっています

AMP(Automatic Mixed Precision)とは、モデルの計算をFP32(単精度)とFP16(半精度)で切り替えて実行する技術。これにより訓練速度向上やGPUメモリ使用量削減が期待できます。Autocast 機能は、この技術を簡単に実装できるように設計されています。この記事では AMP の基本と autocast 機能の使い方について解説します。また、GradScaler を使用することで、精度の低下を回避できます。
torch.distributedの通信操作(broadcast, all_reduce, all_gather, reduce_scatter, scatter, gather, reduceなど)について解説します。通信の種類や用途、実装方法などを紹介します。
PyTorch での分散学習(Distributed Data Parallel, DDP)の実装方法について解説します。分散学習は、GPU の計算リソースを並列化してモデルの学習を高速化する手法です。分散学習には、モデル並列とデータ並列の 2 つの方法があります。この記事では、PyTorch の分散学習機能(DP/DDP)を使用して、これらの実現方法について説明します。
並列学習の種類、分散計算と集合通信概要、DataParallel と DistributedDataParallel の違いについて解説します。
Transformer は、RNN や CNN を排除し、アテンション機構を基盤とするシーケンス処理モデルです。主な要素として、Multi-Head Attention(複数のアテンションヘッドの結合)、位置エンコーディング(sin/cos関数による順序情報付与)が含まれます。エンコーダ・デコーダ構造では、因果マスクで未来情報の参照を制限し、ポジションワイズ FFN や残差接続+レイヤー正規化で学習を安定化します。主要な革新点には、並列計算による高速化、長距離依存関係のモデリング、層構成の拡張性が挙げられ、翻訳や生成など多様なタスクで高性能を発揮します。
この記事では、画像を用いた顔表情認識を例に、PyTorch を使った実践的なタスクの開発プロセスを一から解説します。 第二部となる今回は、PyTorch を使った実装的な技術ポイントを紹介します。
この記事では、PyTorchを使用した画像ベースの顔表情認識システムの開発プロセスを体系的に解説しています。プロジェクト全体の流れ(データ準備→モデル設計→学習→推論)をカバーし、Kaggleの表情データセット(7種類の感情ラベル)を用いた具体的な実装例を提供しています。GitHubリポジトリを通じてコードの再利用性を確保しており、機械学習初心者でも実践的なワークフローを体験できる構成となっています。
PyTorch is an optimized tensor library for deep learning using GPUs and CPUs.
pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118 (CUDA11.8 は必要!!!)最新の pytorch は conda でインストールのをできません。
torch.Tensor(2,3,4).size() # torch.Size([2, 3, 4])
torch.Tensor([2,3,4]).size() # torch.Size([3])
![torch.Tensor(2,3,4) と torch.Tensor([2,3,4])](/assert/dl_pytorch/image/torch_tensor.png)
dtype, requires_gradを指定できない、既存のデータ(リストや NumPy 配列など)からテンソルを作成または未初期化テンソルを作成のための関数data = [1, 2, 3]
tensor = torch.tensor(data, dtype=torch.float32, device='cuda')
tensor = torch.Tensor([1, 2, 3]) # 指定されたデータでテンソルを作成
tensor = torch.Tensor(2, 3) # 2x3の未初期化テンソルを作成
✅ torch.mm:行列積 (Matrix Multiplication)
数学記号:
ここで、、と、C は行列です。
式展開:
>>> A = torch.tensor([[1, 2, 3], [4, 5, 6]]) # shape: (2, 3)
>>> B = torch.tensor([[1, 4], [2, 5], [3, 6]]) # shape: (3, 2)
>>> C = torch.mm(A, B)
>>> C
tensor([[14, 32],
[32, 77]])
✅ torch.mul:要素ごとの積 (Element-wise Multiplication)
数学記号:
ここで、 は同じ形の行列です。
式展開:
>>> A = torch.tensor([[1, 2], [3, 4]]) # shape: (2, 2)
>>> B = torch.tensor([[5, 6], [7, 8]]) # shape: (2, 2)
>>> C = torch.mul(A, B) # shape: (2, 2)
>>> C
tensor([[ 5, 12],
[21, 32]])
以下は PyTorch におけるtorch.stackとtorch.catの使い分けと詳細な説明です:
| 関数 | 動作 | 入力条件 | 出力形状 | 主な用途 |
|---|---|---|---|---|
torch.stack |
新しい次元を追加して結合 | 同じ形状のテンソルのみ | 入力テンソルの形状に新次元追加 | バッチ処理・次元拡張 |
torch.cat |
既存の次元で結合 | 次元数が同じテンソル | 指定次元のサイズが合算 | 特徴量結合・データ連結 |
| 関数 | 作用 |
|---|---|
torch.stack((A, B), dim) |
新しい次元を追加してテンソルを結合(入力テンソルは完全に同一形状である必要あり) |
torch.cat((A, B), dim) |
既存の次元に沿ってテンソルを連結(指定次元のサイズ以外は同一形状である必要あり) |
A = torch.tensor([[1, 2], [3, 4]]) # (2,2)
B = torch.tensor([[5, 6], [7, 8]]) # (2,2)
# dim=0でstack(バッチ次元追加)
C = torch.stack((A, B), dim=0)
print(C.shape) # torch.Size([2, 2, 2])
"""
tensor([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
"""
# dim=1でstack(行方向に結合)
D = torch.stack((A, B), dim=1)
print(D.shape) # torch.Size([2, 2, 2])
"""
tensor([[[1, 2],
[5, 6]],
[[3, 4],
[7, 8]]])
"""
A = torch.randn(2, 3) # (2,3)
B = torch.randn(2, 3) # (2,3)
# dim=0で結合(行方向)
C = torch.cat((A, B), dim=0)
print(C.shape) # torch.Size([4, 3])
# dim=1で結合(列方向)
D = torch.cat((A, B), dim=1)
print(D.shape) # torch.Size([2, 6])
img1 = torch.randn(3, 224, 224) # 画像1(CHW)
img2 = torch.randn(3, 224, 224) # 画像2
batch = torch.stack((img1, img2), dim=0) # バッチ次元追加 (2,3,224,224)
frame1 = torch.randn(256) # 特徴量ベクトル
frame2 = torch.randn(256)
sequence = torch.stack((frame1, frame2), dim=0) # (2,256)
image_features = torch.randn(10, 512) # 画像特徴量
text_features = torch.randn(10, 256) # テキスト特徴量
combined = torch.cat((image_features, text_features), dim=1) # (10,768)
conv_out1 = torch.randn(32, 64, 64)
conv_out2 = torch.randn(32, 64, 64)
merged = torch.cat((conv_out1, conv_out2), dim=0) # (64, 64, 64)
形状の一致要件:
# torch.stackは完全な形状一致が必要
A = torch.rand(2,3)
B = torch.rand(2,3)
torch.stack((A, B)) # OK
A = torch.rand(2,3)
B = torch.rand(3,2)
torch.stack((A, B)) # RuntimeError
次元指定の範囲:
A = torch.rand(2,3)
B = torch.rand(2,3)
torch.stack((A, B), dim=2) # 有効な次元範囲外(0-1)
# IndexError: Dimension out of range
| 操作 | 実行時間(例) | メモリ使用量 |
|---|---|---|
| stack | 1.2ms ± 15µs | 高い(新次元作成) |
| cat | 850µs ± 10µs | 低い(既存次元拡張) |
ここで、画像のデータセットを例にして:
image_numとは、画像はデータセットに何枚あるかを表す。epochとは、データセットを何回学習させるかを表す。iterationとは、毎回 epoch はデータセットを何回読み込むかを表す。batch_sizeとは、毎回 epoch は画像を何枚読み込むかを表す。total_iterationとは、(トレーニング)全体はデータセットを読み込む回数を表す。import torch
print(torch.__version__) # pytorchバージョン
print(torch.version.cuda) # cudaバージョン
print(torch.cuda.is_available()) # cudaが利用可能かどうか
Tensor は numpy の ndarray と同様にデータを格納するデータ構造です。
| データ型 | CPU Tensor | GPU Tensor |
|---|---|---|
| 8 ビット符号なし整数型 | torch.ByteTensor |
torch.cuda.ByteTensor |
| 8 ビット符号付き整数型 | torch.CharTensor |
torch.cuda.CharTensor |
| 16 ビット符号付き整数型 | torch.ShortTensor |
torch.cuda.ShortTensor |
| 32 ビット符号付き整数型 | torch.IntTensor |
torch.cuda.IntTensor |
| 64 ビット符号付き整数型 | torch.LongTensor |
torch.cuda.LongTensor |
| 32 ビット浮動小数点数型 | torch.FloatTensor |
torch.cuda.FloatTensor |
| 64 ビット浮動小数点数型 | torch.DoubleTensor |
torch.cuda.DoubleTensor |
| ブール型 | torch.BoolTensor |
torch.cuda.BoolTensor |
torch.cuda.FloatTensor は GPU 上での 32 ビット浮動小数点数型を表します。)
>>> a = np.random.randn(2,3)
>>> a
array([[ 0.55657307, -0.56752282, -1.29813938],
[ 0.19568811, -1.58711887, 0.96234087]])
>>> t = torch.tensor(a, dtype=torch.float32, device=torch.device('cuda:2'))
>>> t
tensor([[ 0.5566, -0.5675, -1.2981],
[ 0.1957, -1.5871, 0.9623]], device='cuda:2')
>>> torch.randn([2,3])
tensor([[-0.4271, 1.0660, 1.2755],
[-1.5805, 0.4410, 0.4207]])
>>> torch.randn([2,3], dtype=torch.float64, device='cuda')
tensor([[-0.8559, 1.0472, 0.6330],
[-0.5150, -0.8062, -2.4052]], device='cuda:0', dtype=torch.float64)
>>> torch.randint(0, 10, [2,3])
tensor([[5, 7, 5],
[0, 7, 9]])
>>> torch.randint(0, 10, [2,3], dtype=torch.int8, device='cuda')
tensor([[7, 8, 6],
[7, 5, 2]], device='cuda:0', dtype=torch.int8)
>>> torch.randint(0, 10, [2,3]).dtype
torch.int64
| 関数 | 作用 |
|---|---|
torch.abs(A) |
絶対値を計算する |
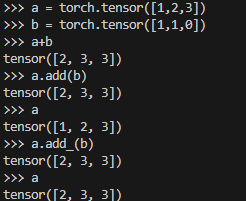
torch.add(A, B) |
加算を行う。A と B は Tensor またはスカラーのいずれでも可能 |
torch.clamp(A, min, max) |
クリップ(範囲制限)。A のデータがminより小さいかmaxより大きい場合、minまたはmaxに変換され、範囲を[min, max]に保つ |
torch.div(A, B) |
除算を行う。A / B。A と B は Tensor またはスカラーのいずれでも可能 |
torch.mul(A, B) |
要素ごとの乗算(点乗算)。A * B。A と B は Tensor またはスカラーのいずれでも可能 |
torch.pow(A, n) |
べき乗を計算する。A の n 乗 |
torch.mm(A, B.T) |
行列の乗算(行列積)。torch.mulとの違いに注意 |
torch.mv(A, B) |
行列とベクトルの乗算。A は行列、B はベクトル。B は転置の必要はない |
A.item() |
Tensor を基本データ型に変換する。Tensor に要素が 1 つしかない場合に使用可能。主に Tensor から数値を取り出すために使用 |
A.numpy() |
Tensor を Numpy 型に変換する |
A.size() |
サイズを確認する |
A.shape |
サイズを確認する |
A.dtype |
データ型を確認する |
A.view() |
テンソルのサイズを再構築する。Numpy のreshapeに類似 |
A.transpose(0, 1) |
行と列を交換する |
A[1:] |
スライス。Numpy のスライスに類似 |
A[-1, -1] = 100 |
スライス。Numpy のスライスに類似 |
A.zero_() |
ゼロ化する(すべての要素を 0 にする) |
torch.stack((A, B), dim=-1) |
テンソルを結合し、次元を増やす |
torch.diag(A) |
A の対角要素を取り出し、1 次元ベクトルを形成する |
torch.diag_embed(A) |
1 次元ベクトルを対角線に配置し、残りの要素を 0 とするテンソルを作成する |
torch.unqueeze(A, dim) |
テンソルの指定した次元に要素を追加する |
import torch
# GPU環境が利用可能かテスト
print(torch.__version__) # PyTorchのバージョン確認
print(torch.version.cuda) # CUDAのバージョン確認
print(torch.cuda.is_available()) # CUDAが利用可能か確認
# GPUまたはCPUのデバイス選択
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# オブジェクトの実行環境を確認
a.device # テンソルaが存在するデバイスを表示
# オブジェクトを指定デバイスに転送
A = A.to(device) # テンソルAを選択したデバイス環境に設定
# オブジェクトをCPU環境に転送
A.cpu().device # テンソルAをCPU環境に移動
# 異なるデバイス間での演算時の自動変換
a + b.to(device) # デバイス環境が混在する場合、bのデバイス環境に統一される
# CUDAテンソルからnumpyへの変換手順
a.cpu().numpy() # CUDAテンソルはCPU経由でnumpyに変換する必要あり
# CUDA型テンソルの作成
torch.tensor([1,2], device=device) # 指定デバイス上に直接テンソルを作成
nvidia-smiで GPU の状態を確認するtorch.cuda.is_available()で GPU が利用可能か確認するtorch.cuda.empty_cache()でメモリを解放するtorch.cuda.device_count()で GPU の数を確認するtorch.cuda.get_device_name(0)で GPU の名前を確認するtorch.cuda.current_device()で現在の GPU を確認する(おもに multi-gpus をつかう場合)Autograd は自動微分のこと。つまり、関数の値や勾配を自動で計算する。
自動微分(Automatic Differentiation)はディープラーニングフレームワークの中核機能で、数学関数の導関数を自動的に計算します。
連鎖律(Chain Rule)に基づき、複合関数の導関数を効率的に計算します。PyTorch のモデルは多くの層で構成される複雑な関数のため、Autograd が各層の勾配を効率的に計算します。
| 種類 | 特徴 | フレームワーク例 |
|---|---|---|
| 動的計算グラフ | 実行時にグラフを構築(デバッグ・変更が容易) | PyTorch |
| 静的計算グラフ | 実行前にグラフを構築(最適化が可能) | TensorFlow(初期版) |
torch.Tensorオブジェクトのrequires_grad属性で勾配計算の有無を制御:
# 勾配計算が必要なテンソル作成
x = torch.randn(2, 2, requires_grad=True)
print(x)
# tensor([[-0.5736, -0.2012],
# [ 1.3563, 0.5499]], requires_grad=True)
# 演算の追跡
y = x + 2
z = y * y * 3
out = z.mean()
print(out)
# tensor(17.2779, grad_fn=<MeanBackward0>)
.backward()メソッドで勾配計算:
out.backward() # 勾配計算
print(x.grad) # 勾配値の確認
# tensor([[2.1396, 2.6982],
# [5.0345, 3.8248]])
以下の方法で勾配計算を停止可能:
# 方法1: コンテキストマネージャー
with torch.no_grad():
y = x * 2
# 方法2: メソッドの引数
@torch.no_grad()
def inference():
y = x * 2
return y
# 方法3: 属性設定
print(x.requires_grad)
# True
x.requires_grad_(False)
# tensor([[-0.5736, -0.2012],
# [ 1.3563, 0.5499]])
print(x.requires_grad)
# False
| メソッド | 説明 |
|---|---|
.backward() |
勾配を自動計算 |
.detach() |
勾配追跡から切り離したテンソルを生成 |
torch.no_grad() |
勾配計算を無効にするコンテキスト |
.retain_grad() |
非リーフテンソルの勾配を保持 |
from torch.utils.data import DataLoader, Dataset
# Datasetの基本構造
class CustomDataset(Dataset):
def __init__(self, data, targets):
self.data = data
self.targets = targets
def __getitem__(self, index):
return self.data[index], self.targets[index]
def __len__(self):
return len(self.data)
# DataLoaderの基本使用例
train_dataset = CustomDataset(data_samples, target_labels)
train_loader = DataLoader(
dataset=train_dataset,
batch_size=64,
shuffle=True,
num_workers=4
)
# 実行ループ例
for epoch in range(num_epochs):
for batch_data, batch_labels in train_loader:
batch_data = batch_data.to(device)
batch_labels = batch_labels.to(device)
...
役割
データセットの抽象基底クラス。データの読み込みと前処理をカプセル化し、データアクセスを一貫性のある方法で提供します。
必須メソッド
__getitem__(self, index): 指定インデックスのデータサンプルを返す__len__(self): データセットの総サンプル数を返す特徴
# DataLoaderの主要パラメータとその説明(橙色部分重点)
from torch.utils.data import DataLoader, Dataset
class SampleDataset(Dataset):
def __init__(self):
self.data = [...] # データセットの初期化
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
# データローダーの実用的設定例
train_loader = DataLoader(
dataset=SampleDataset(), # [必須] 使用するDatasetオブジェクト
batch_size=32, # [重要] バッチサイズ(デフォルト1)
shuffle=True, # [重要] エポックごとにデータをシャッフル(学習時はTrue推奨)
num_workers=4, # [重要] データ読み込みの並列プロセス数(0でシングルスレッド)
collate_fn=None, # [応用] カスタムバッチ作成関数(不規則データ用)
pin_memory=True, # [GPU推奨] CUDAへの高速転送を可能にする
drop_last=False # [調整] 最後の不完全バッチを削除するか(デフォルトFalse)
)
| パラメータ | 役割と設定例 | 最適化のポイント |
|---|---|---|
| dataset | データソースとなる Dataset オブジェクト(必須) | 自作 Dataset クラスか torchvision.datasets 等の既存データセットを使用する |
| batch_size | 1 イテレーションあたりのサンプル数 | GPU メモリ容量とトレードオフ (例:32/64/128/256) |
| shuffle | エポックごとにデータをランダムシャッフルするか | 学習時は True で過学習防止 評価時は False で安定化 |
| num_workers | データ読み込み用プロセス数(I/O 並列化) | CPU リソース許す限り増やす(例:4-8)num_workers=0はシングルスレッド |
| collate_fn | バッチ作成時のカスタム処理(不規則形状データ用) | 画像とテキストの組み合わせなど、形状が異なるデータをバッチ化する際に必要 |
| pin_memory | CUDA への転送速度向上(ページ锁定メモリ使用) | GPU 環境では必ず True に設定 (CPU→GPU 転送速度が約 2 倍速くなる) |
| drop_last | 最後の不完全バッチを削除するか | バッチ処理が厳密なサイズ要求の場合は True (例:特定のモデルアーキテクチャ) |
# GPU環境向け最適設定例
dataloader = DataLoader(
dataset=train_dataset,
batch_size=64, # GPUメモリ許容範囲で最大限設定
shuffle=True,
num_workers=4, # CPUコア数に応じて調整
pin_memory=True, # CUDA環境必須
drop_last=False # データロスを許容できない場合
)
# データオーギメンテーション付き例
from torchvision import transforms
test_dataset = MyDataset(transform=transforms.Compose([...]))
test_loader = DataLoader(
dataset=test_dataset,
batch_size=16,
shuffle=False,
num_workers=2,
collate_fn=my_custom_collate # 不規則データ用
)
num_workers の最適化
pin_memory の効果
バッチサイズのトレードオフ
collate_fn の使用ケース
特徴
PyTorch はtorch.nn.Moduleクラスを通じてニューラルネットワーク構築の便利なインターフェースを提供します。nn.Module クラスを継承し、独自のネットワーク層を定義することができます。
import torch.nn as nn
import torch.optim as optim
# 全結合ニューラルネットワークの定義
class SimpleNN(nn.Module):
def __init__(self):
super(SimpleNN, self).__init__()
self.fc1 = nn.Linear(1024, 224) # 入力層から隠れ層へ
self.fc2 = nn.Linear(224, 10) # 隠れ層から出力層へ
def forward(self, x):
x = torch.relu(self.fc1(x)) # ReLU活性化関数
x = self.fc2(x)
return x
# ネットワークインスタンスの作成
model = SimpleNN()
# モデル構造の表示
print(model)
nn.Moduleを継承してネットワーククラスを定義__init__メソッドで層を初期化forwardメソッドでデータの流れを定義SimpleNN(
(fc1): Linear(in_features=1024, out_features=224, bias=True)
(fc2): Linear(in_features=224, out_features=10, bias=True)
)
ニューラルネットワークはニューロン間の接続重みを調整することで予測結果を最適化し、このプロセスには以下の要素が含まれます:
# 実行ループ例
model.train() # モデルを学習モードに設定
for epoch in range(num_epochs):
for batch_data, batch_labels in train_loader: # バッチデータを取得
batch_data = batch_data.to(device)
batch_labels = batch_labels.to(device)
outputs = model(batch_data) # 順伝播
loss = criterion(outputs, batch_labels) # 損失計算
loss.backward() # 逆伝播とパラメータ更新(簡単の例)
主なニューラルネットワークの種類と用途:
| 種類 | 用途例 |
|---|---|
| フィードフォワードネットワーク | 基本的なパターン認識 |
| 畳み込みニューラルネットワーク(CNN) | 画像認識、物体検出 |
| リカレントニューラルネットワーク(RNN) | 時系列データ分析、自然言語処理 |
| LSTM ネットワーク | 長期依存関係のある時系列データ処理 |
損失(Loss)の役割
主な損失関数の種類
| 損失関数クラス | 数学式 | 主な用途 | 入力形式要件 |
|---|---|---|---|
nn.MSELoss |
回帰問題 | 連続値(任意形状) | |
nn.CrossEntropyLoss |
多クラス分類 | ロジット値(未正規化) | |
nn.BCELoss |
二値分類 | 確率値(0-1 範囲) | |
nn.L1Loss |
ロバスト回帰 | 連続値(任意形状) | |
nn.TripletMarginLoss |
類似度学習 | 3 組の埋め込みベクトル |
# 代表的な損失関数の使用例
import torch.nn as nn
# 平均二乗誤差(回帰問題用)
mse_loss = nn.MSELoss()
output = model(inputs)
loss = mse_loss(output, targets)
# 交差エントロピー(分類問題用)
ce_loss = nn.CrossEntropyLoss()
output = model(inputs)
loss = ce_loss(output, targets)
# バイナリ交差エントロピー(二値分類用)
bce_loss = nn.BCELoss()
output = torch.sigmoid(model(inputs)) # 確率値に変換
loss = bce_loss(output, targets.float())
# 方法1: nn.Moduleを継承
class CustomLoss(nn.Module):
def __init__(self, alpha=0.5):
super().__init__()
self.alpha = alpha
def forward(self, pred, target):
mse = torch.mean((pred - target)**2)
l1 = torch.mean(torch.abs(pred - target))
return self.alpha * mse + (1 - self.alpha) * l1
# 方法2: 関数形式
def custom_loss(pred, target, beta=0.3):
base_loss = F.binary_cross_entropy(pred, target)
penalty = torch.mean(torch.relu(pred - 0.7))**2
return base_loss + beta * penalty
# マルチタスク学習用の複合損失
class MultiTaskLoss(nn.Module):
def __init__(self):
super().__init__()
self.ce = nn.CrossEntropyLoss()
self.mse = nn.MSELoss()
def forward(self, pred_class, pred_reg, target_class, target_reg):
loss1 = self.ce(pred_class, target_class)
loss2 = self.mse(pred_reg, target_reg)
return loss1 + 0.5*loss2 # 重み付け加算
# 学習ループ内での利用
criterion = MultiTaskLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(epochs):
for data, (labels_class, labels_reg) in train_loader:
outputs_class, outputs_reg = model(data)
loss = criterion(outputs_class, outputs_reg, labels_class, labels_reg)
optimizer.zero_grad()
loss.backward()
optimizer.step()
| 問題タイプ | 推奨損失関数 | 補足事項 |
|---|---|---|
| 回帰問題 | MSELoss / HuberLoss |
外れ値が多い場合は HuberLoss が安定 |
| 多クラス分類 | CrossEntropyLoss |
出力層の直前に Softmax 不要(組み込み済み) |
| 二値分類 | BCELoss |
出力をシグモイドで確率値に変換する必要あり |
| マルチラベル分類 | BCEWithLogitsLoss |
シグモイド+BCELoss を組み合わせた効率的な実装 |
| 不均衡データ分類 | 重み付きCrossEntropyLoss |
クラスごとのサンプル数に応じて重み設定 |
| 物体検出 | SmoothL1Loss |
バウンディングボックス回帰に有効 |
カスタム損失の微分保証
メモリ効率最適化
# メモリ節約テクニック
loss = criterion(output, target)
loss.backward() # 勾配計算
optimizer.step() # パラメータ更新
optimizer.zero_grad() # 勾配リセット(重要!)
複数損失の組み合わせ
# 複数損失を個別に計算する例
loss1 = criterion1(output1, target1) * weight1
loss2 = criterion2(output2, target2) * weight2
total_loss = loss1 + loss2
total_loss.backward()
# 主要オプティマイザの使用例
import torch.optim as optim
# モデルパラメータとオプティマイザの初期化
model = SimpleNN()
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-4)
# 学習ループでの使用
for epoch in range(epochs):
for data, target in train_loader:
optimizer.zero_grad() # 勾配のリセット
output = model(data)
loss = criterion(output, target)
loss.backward() # 勾配計算
optimizer.step() # パラメータ更新
パラメータ更新メカニズム
主要オプティマイザの比較
| オプティマイザ | メリット | デメリット | 最適な使用ケース |
|---|---|---|---|
| SGD | シンプル、メモリ効率良好 | 収束が遅い | 小規模データセット |
| Adam | 高速収束、ハイパラ調整少 | メモリ使用多 | 深層学習全般 |
| RMSprop | 不安定な勾配に強い | 学習率調整必要 | RNN/LSTM |
| Adagrad | 特徴頻度適応型 | 学習率急速低下 | スパースデータ |
| Adadelta | 学習率自動調整 | 計算コスト高 | 長期依存関係 |
共通パラメータ
optimizer = optim.Adam(
params=model.parameters(), # 必須:最適化対象パラメータ
lr=0.001, # 学習率(デフォルト値あり)
betas=(0.9, 0.999), # モーメンタム係数(Adam専用)
weight_decay=0.01, # L2正則化係数
amsgrad=False # AMSGrad変種(Adam専用)
)
# パラメータグループの分割
optimizer = optim.SGD([
{'params': model.base.parameters(), 'lr': 0.001},
{'params': model.classifier.parameters(), 'lr': 0.01}
], momentum=0.9)
# 学習率スケジューラとの連携
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
# 勾配のノルム制限
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
optimizer.step()
| オプティマイザ | 更新式(簡略版) |
|---|---|
| SGD | |
| Momentum | |
| Adam |
学習率のウォームアップ
# 初期数エポックで学習率を徐々に増加
warmup_epochs = 5
for epoch in range(epochs):
lr = base_lr * min(epoch / warmup_epochs, 1.0)
for param_group in optimizer.param_groups:
param_group['lr'] = lr
# 通常の学習処理...
勾配蓄積(メモリ不足時)
accumulation_steps = 4
for i, (data, target) in enumerate(train_loader):
output = model(data)
loss = criterion(output, target)
loss = loss / accumulation_steps # 損失のスケーリング
loss.backward()
if (i+1) % accumulation_steps == 0:
optimizer.step()
optimizer.zero_grad()
混合精度トレーニング
scaler = torch.cuda.amp.GradScaler()
for data, target in train_loader:
optimizer.zero_grad()
with torch.cuda.amp.autocast():
output = model(data)
loss = criterion(output, target)
scaler.scale(loss).backward()
scaler.step(optimizer)
scaler.update()
勾配の未リセット
# 誤り例
output = model(input)
loss.backward()
optimizer.step() # 勾配が蓄積される
# 正しい例
optimizer.zero_grad()
output = model(input)
loss.backward()
optimizer.step()
パラメータグループの誤指定
# 誤り例(重み減衰の不適切適用)
optimizer = Adam(model.parameters(), weight_decay=1e-4) # BatchNorm層にも適用される
# 正しい例
params = [
{'params': model.features.parameters(), 'weight_decay': 1e-4},
{'params': model.bn.parameters(), 'weight_decay': 0}
]
optimizer = Adam(params, lr=0.001)
学習率スケジューラの誤使用
# 誤り例(ステップ位置不適切)
optimizer.step()
scheduler.step() # エポック終了時に実行するべき
# 正しい例
for epoch in range(epochs):
for batch in train_loader:
# ...学習処理...
optimizer.step()
scheduler.step()
PyTorch のlr_scheduler(学習率スケジューラ)は、ニューラルネットワークの訓練中に学習率を動的に調整するための仕組みです。これにより、収束速度やモデル性能を向上させることが可能になります。
| クラス名 | 説明 |
|---|---|
StepLR |
一定エポックごとに学習率を減少(gamma 倍) |
MultiStepLR |
指定した複数のエポックで学習率を減少 |
ExponentialLR |
各エポックで学習率を指数関数的に減少 |
CosineAnnealingLR |
コサイン減衰に従って学習率を変化 |
ReduceLROnPlateau |
検証損失が改善しなくなったときに学習率を減少 |
CyclicLR |
学習率を周期的に増減させる |
OneCycleLR |
エポック内で 1 回だけ学習率を上げ下げする(高性能) |
import torch
from torch.optim import SGD
from torch.optim.lr_scheduler import StepLR
model = ... # モデル定義
optimizer = SGD(model.parameters(), lr=0.1)
scheduler = StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(100):
for input, target in dataloader:
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
scheduler.step() # エポックごとに呼び出す
from torch.optim.lr_scheduler import ReduceLROnPlateau
scheduler = ReduceLROnPlateau(optimizer, 'min', patience=5)
for epoch in range(epochs):
train(...)
val_loss = validate(...)
scheduler.step(val_loss) # 検証ロスを与える
Sets the learning rate of each parameter group according to the 1cycle learning rate policy.
from torch.optim.lr_scheduler import OneCycleLR
scheduler = OneCycleLR(
optimizer,
max_lr=0.01,
steps_per_epoch=len(dataloader),
epochs=num_epochs
)
for epoch in range(num_epochs):
for batch in dataloader:
...
scheduler.step()
scheduler.step() は通常 各エポック終了時に 1 回だけ呼び出すstate_dict() を使う# スケジューラの設定
warmup_epochs = 5
total_epochs = 100
# Cosine Annealing スケジューラ (warmup設定)
lr_scheduler = CosineAnnealingLR(
optimizer,
max_epochs=total_epochs,
warmup_epochs=warmup_epochs,
warmup_start_lr=0.0001,
eta_min=0.00001
)
Hexoでカテゴリとタグの追加方法を解説します。カテゴリページ、タグページの生成から記事へのcategories属性・tags属性の追加まで網羅しています。