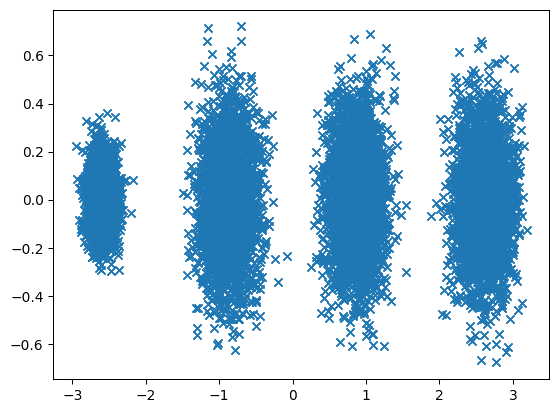数学基礎

固有値と固有ベクトル

もしベクトル$v$が行列$A$の固有ベクトルであれば、必ず以下の形式で表すことができます：

$Av=\lambda v$

ここで：

• $λ$ は固有ベクトル$v$に対応する固有値
• ある行列の固有ベクトルの組は直交ベクトルの組です

重要な性質

• 固有ベクトルは行列の変換に対して方向を変えない（スカラー倍されるだけ）
• 固有値はその方向における変換の「伸縮率」を表す

固有値分解行列

行列$A$について、一連の固有ベクトル$v$があり、このベクトルを正規直交化すると、一連の正規直交単位ベクトルが得られます。固有値分解とは、行列$A$を以下の式のように分解することです：

$A=Q\Sigma Q^{-1}$

ここで：

• $Q$ は行列$A$の固有ベクトルで構成される行列
• $\Sigma$ は対角行列で、対角線上の要素は固有値

実対称行列の場合

実対称行列（例えば共分散行列）の場合、$Q$ は直交行列となるため、$Q^{-1} = Q^T$ となり：

$A=Q\Sigma Q^T$

PCAとの関係

• PCAでは、共分散行列の固有値分解を行い、最大の固有値に対応する固有ベクトル（主成分）を選択
• 固有値の大きさは、その主成分方向のデータの分散の大きさを示す
• 固有ベクトルは主成分の方向を表す

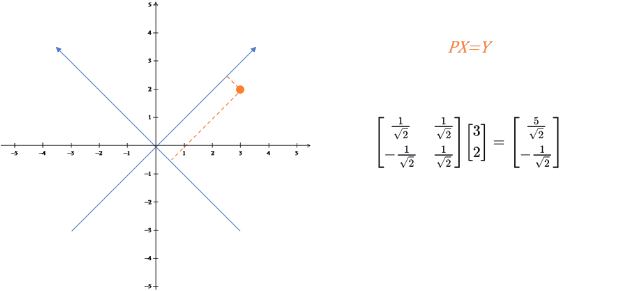
基底変換

数式表現

$Y = PX = \begin{bmatrix} p_1 \\ p_2 \\ \vdots \\ p_r \end{bmatrix}_{r\times n}[ \begin{array} {cccccc}x_1 & x_2 & \cdots & x_m \end{array}]_{n\times m}= \begin{bmatrix} p_1x_1 & p_1x_2 & \cdots & p_1x_m \\ p_2x_1 & p_2x_2 & \cdots & p_2x_m \\ \vdots & \vdots & \ddots & \vdots \\ p_rx_1 & p_rx_2 & \cdots & p_rx_m \end{bmatrix}_{r\times m}$

• 元の基底：$ {[p_1, p_2, …, p_n]}^T $
• 新しい基底：$ {[x_1, x_2, …, x_m]} $
• 座標変換：$ P $ が旧座標系でのベクトル、$ x $ が新座標系でのベクトルなら、$ Y = PX $

本質

行列掛け算の本質は基底変換である。

基底変換と座標系の伸長と回転

座標系の伸長

$Y = XP$

$P = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}$

例

$X = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad P = \begin{bmatrix} 2 & 0 \\ 0 & 0.5 \end{bmatrix}$

$Y = XP = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & 0.5 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 6 & 2 \end{bmatrix}$

この例では、第1特徴量を2倍に伸長し、第2特徴量を0.5倍に縮小しています。

座標系の回転

$Y = RX$

$R = \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}$

分散

分散は数値が平均値からどれだけ散らばっているかを示す指標です。

数式：

$\text{Var}(X) = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2$

ここで：

• $ x_i $：個々のデータ点
• $ \bar{x} $：データの平均
• $ n $：データ点の数

共分散

共分散は2つの変数が一緒にどう変化するかを測る指標で、同時に増加する傾向があるかを示します。

数式

$\text{Cov}(X,Y) = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})$

ここで：

• $ x_i, y_i $：2つの異なる変数のデータ点
• $ \bar{x}, \bar{y} $：それぞれの変数の平均

解釈：

• 正の共分散：変数が一緒に増加する傾向
• 負の共分散：一方が増えると他方は減る
• ゼロの共分散：線形関係なし

本質：共分散行列は、各変数の共分散を対角要素として持つ矩形行列です、共分散は $0$ の場合、二つの変数は完全に関係ない。

共分散行列

共分散行列は多変量データセットの各次元ペア間の共分散を含む正方行列です。

数式

先ず要するに、行列$X_{n \times m}$の共分散行列数式は：

$C=\frac{1}{m-1} XX^T$

手順は以下通り：

1. サンプル平均

$\bar{x}=\frac{1}{n}\sum_{i=1}^{N}{x_{i}}$

2. サンプル分散

$Var(x)=S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}{\left( x_{i}-\bar{x} \right)^2}$

3. サンプルの共分散

$Cov(x,y)=\frac{1}{n-1}\sum_{i=1}^{n}{\left( x_{i}-\bar{x} \right)\left( y_{i}-\bar{y} \right)}$

4. サンプルの共分散行列

ここで、$dim=2$のベクトル${[x,y]}^T$にしては：

$C= \begin{bmatrix} Var(x) & Cov(x,y) \\ Cov(x,y) & Var(y) \end{bmatrix}$

$dim=n$のベクトル${[x_1,x_2,...,x_n]}^T$にしては：

$C= \begin{bmatrix} Var(x_1) & Cov(x_1,x_2) & \cdots & Cov(x_1,x_n) \\ Cov(x_2,x_1) & Var(x_2) & \cdots & Cov(x_1,x_n) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(x_n,x_1) & Cov(x_n,x_2) & \cdots & Var(x_n) \end{bmatrix}$

SVD

SVDの定義

特異値分解は、任意の行列に適用可能な分解方法であり、任意の行列Aに対して常に特異値分解が存在します。

数式表現

$A = U \Sigma V^T$

ここで：

• A：$m \times n$ の行列
• U：$m \times m$ の直交行列（左特異ベクトル）
• Σ：$m \times n$ の行列（対角線上以外はすべて0、対角線上の要素は特異値）
• V^T：$n \times n$ の直交行列の転置（右特異ベクトル）

SVD分解の手順

1. $AA^T$ の固有値と固有ベクトルを求める
   • $AA^T$ の固有値と固有ベクトルを計算
   • 固有ベクトルを正規化して行列 U を構成
2. $A^TA$ の固有値と固有ベクトルを求める
   • $A^TA$ の固有値と固有ベクトルを計算
   • 固有ベクトルを正規化して行列 V を構成
3. 特異値の計算
   • $AA^T$ または $A^TA$ の固有値の平方根を計算
   • その値を対角要素として行列 Σ を構成

重要な特徴

• 特異値は通常、大きい順に並べられます
• U は左特異ベクトル（$AA^T$ の固有ベクトル）
• V は右特異ベクトル（$A^TA$ の固有ベクトル）
• Σ の対角要素が特異値であり、行列Aの「重要度」を示します

PCA

PCA（主成分分析）は主成分を抽出するための手法である。主成分はデータの分散を最大にするベクトルである。

共分散行列対角化

ここで、二つの行列$Y_{r \times m}$と$X_{n \times m}$がある。

そして、

1. $P_{r \times n}$があり、$$Y_{r \times m}=P_{r \times n}X_{n \times m}$$
2. $C$は$X$の共分散行列、$D$は$Y$の共分散行列である

目的: 元のデータ $X$ にPCAを適用した後、得られる $Y$ の共分散行列 $D$ の各方向の分散が最大になり、共分散が $0$ になることです。

では、$C$ と $D$ はどのような関係にあるのでしょうか：

$D = \frac{1}{m}YY^T \\ = \frac{1}{m}(PX)(PX)^T \\ = \frac{1}{m}PXX^TP^T \\ = \frac{1}{m}P(XX^T)P^T \\ = PCP^T \\ = P \begin{bmatrix} \frac{1}{m}\sum_{i=1}^{m} x_{1i}^2 & \frac{1}{m}\sum_{i=1}^{m} x_{1i}x_{2i} \\ \frac{1}{m}\sum_{i=1}^{m} x_{2i}x_{1i} & \frac{1}{m}\sum_{i=1}^{m} x_{2i}^2 \end{bmatrix} P^T$

ここに計算するところ、求めている $P$ は、元の共分散行列を対角化する $P$ であることを発見しました。

言い換えれば、最適化目標は行列 $P$ を見つけることであり、$P C P^T$ が対角行列であり、対角要素が大きい順に並んでいることを満たす必要があります。すると、$P$ の上位 $r$ 行が求めている基底となり、$P$ の上位 $r$ 行で構成される行列に $X$ を乗じることで、$X$ が $n$ 次元から $r$ 次元に削減され、上記の最適化条件を満たします。

ここで最後に、共分散行列の対角化という問題に集中することになります。

上記より、$X$ の共分散行列 $C$ は対称行列であることがわかります。線形代数において、実対称行列には非常に良い性質があります：

1. 実対称行列の異なる固有値に対応する固有ベクトルは必ず直交する。

2. 固有ベクトル $λ_i$ の重複度が $k_i$ であれば、$k_i$ 個の線形独立な固有ベクトルが存在し、それらを正規直交化できます。

上記2つの性質より、$n \times n$ の実対称行列には必ず $n$ 個の単位直交固有ベクトルを見つけることができ、これらを $e_1, e_2, ..., e_n$ とし、列として行列を構成します：

$E = [e_1, e_2, ..., e_n]$

xの共分散行列 $C$ について以下の結論があります：

$E^TCE = \Lambda = \begin{bmatrix} \lambda_1 & 0 & 0 & ... & 0 \\ 0 & \lambda_2 & 0 & ... & 0 \\ 0 & 0 & \lambda_3 & ... & 0 \\ 0 & 0 & 0 & ... & 0 \\ 0 & 0 & 0 & ... & \lambda_n \end{bmatrix}$

ここで、$\Lambda$ は対角行列であり、対角要素は各固有ベクトルに対応する固有値（重複もあり得る）です。

上記の式より：

$D=P C P^T$

$D$ は対角行列であり、以下を得ます：

$P = E^T$

は共分散行列の固有ベクトルを単位化して行方向に並べた行列で、各行は $C$ の固有ベクトルです。もし $P$ を $\Lambda$ 内の固有値の大きい順に、固有ベクトルを上から下に並べると、$P$ の上位 $r$ 行で構成される行列に元のデータ行列 $X$ を乗じることで、求めている次元削減後のデータ行列 $Y$ が得られます。

固有値分解による共分散行列のPCA実装

入力

データセット $X=\left\{ x_{1},x_{2},x_{3},...,x_{n} \right\}$、k次元に削減する必要がある。

手順

1. 平均値の除去（中心化）：各特徴量からそれぞれの平均値を引く

2. 共分散行列の計算：$\frac{1}{n}XX^T$（注：標本数nまたはn-1で割るかは、求められる固有ベクトルには影響しない）

3. 固有値分解：共分散行列 $\frac{1}{n}XX^T$ の固有値と固有ベクトルを求める

4. ソートと選択：固有値を大きい順に並べ替え、最大のk個を選ぶ。対応するk個の固有ベクトルを行ベクトルとして構成される行列Pを得る

5. 変換：データをk個の固有ベクトルで構築された新しい空間に変換する：$Y=PX$

例

$X=\left( \begin{matrix} -1 & -1 &0&2&0\\ -2&0&0&1&1 \end{matrix} \right)$

この2行のデータを1行に削減するPCAの例：

1. X行列の各行はすでにゼロ平均であるため、平均値の除去は不要

2. 共分散行列の計算：

$C=\frac{1}{5}\left( \begin{matrix} -1&-1&0&2&0\\ -2&0&0&1&1 \end{matrix} \right) \left( \begin{matrix} -1&-2\\ -1&0\\ 0&0\\ 2&1\\ 0&1 \end{matrix} \right) = \left( \begin{matrix} \frac{6}{5}&\frac{4}{5}\\ \frac{4}{5}&\frac{6}{5} \end{matrix} \right)$

3. 共分散行列の固有値と固有ベクトルの計算：

   • 固有値：$\lambda_{1}=2$、$\lambda_{2}=\frac{2}{5}$
   • 固有ベクトル：$c_{1} \left( \begin{matrix} 1\\ 1 \end{matrix} \right)$、$c_{2} \left( \begin{matrix} -1\\ 1 \end{matrix} \right)$
   • 標準化された固有ベクトル：$\left( \begin{matrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{matrix} \right)$、$\left( \begin{matrix} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{matrix} \right)$

4. 行列P：

$P=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \end{matrix} \right)$

5. 最後にPの1行目でデータ行列Xを乗じて、次元削減された結果を得る：

$Y=\left( \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{matrix} \right) \left( \begin{matrix} -1 & -1& 0&2&0\\ -2&0&0&1&1 \end{matrix} \right) = \left( \begin{matrix} -\frac{3}{\sqrt{2}} & - \frac{1}{\sqrt{2}} &0&\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{matrix} \right)$

注意：固有値分解による共分散行列の方法では、データ行列Xの行（または列）方向の1つのPCA削減方向しか得られない。

SVD分解による共分散行列のPCA実装

入力

データセット $X=\left\{ x_{1},x_{2},x_{3},...,x_{n} \right\}$、k次元に削減する必要がある。

手順

1. 平均値の除去：各特徴量からそれぞれの平均値を引く

2. 共分散行列の計算

3. SVDによる固有値と固有ベクトルの計算

4. ソートと選択：固有値を大きい順に並べ替え、最大のk個を選ぶ。対応するk個の固有ベクトルを列ベクトルとして構成される行列を得る

5. 変換：データをk個の固有ベクトルで構築された新しい空間に変換する

SVDの利点

PCA削減では、サンプル共分散行列 $XX^T$ の最大k個の固有ベクトルを見つけ、これらで構成される行列で低次元投影を行う必要がある。この過程では、共分散行列 $XX^T$ を求めなければならないが、サンプル数も特徴数も多い場合、計算量は非常に大きい。

SVD分解でPCAを実装する場合の2つの利点：

1. 計算効率：一部のSVD実装アルゴリズムでは、共分散行列 $XX^T$ を求めずに右特異行列Vを求めることができる。つまり、PCAアルゴリズムは固有値分解ではなくSVDで実現でき、この方法はサンプル数が多い場合に効果的。実際、scikit-learnのPCAアルゴリズムの背後ではSVDが使用されており、固有値分解ではない。

2. 双方向のPCA削減：PCAではSVDの左特異行列のみを使用し、右特異行列は使用しないが、右特異行列にも用途がある。

$m \times n$ の行列Xがある場合、SVDによって行列 $X^TX$ の最大k個の固有ベクトルで構成される $k \times n$ の行列 $V^T$ を見つけたとすると：

$X_{m \times k}^{'}=X_{m \times n}V_{n \times k}^{T}$

$m \times k$ の行列X’が得られ、元の $m \times n$ 行列Xと比較して列数がnからkに削減されている。つまり、左特異行列は行数の圧縮に使用できる。右特異行列は列（特徴次元）の圧縮に使用できる。このように、SVD分解でPCAを実装することで、2方向のPCA削減（行と列の2方向）を得ることができる。

PCAの本質

なお、PCAの目的を考え、“元のデータ $X$ にPCAを適用した後、得られる $Y$ の共分散行列 $D$ の各方向の分散が最大になり、共分散が $0$ になることです”ということには、“共分散数が$0$”つまり$Y$の各緯度のベクトル$\{y_1, y_2,...,y_n\}$は関係なく、“共分散行列の各方向の分散最大”つまり区分安くなるということです。

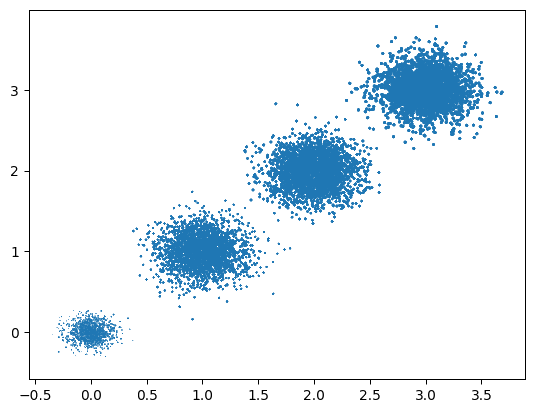
PCA前のデータ

PCA後のデータ

• 任意のデータ投影の第1の分散が第1座標（第1主成分）に来る
• 第2の分散が第2座標（第2主成分）に来る
• $Y = PX$の本質は座標系の変換

コード

code