Swin Transformer
目次
- Vision Transformerの課題
- Patch Embedding
- ウィンドウ分割 (Window Partition)
- W-MSA (Windwow multi-head self attentio)
- SW-MSA (Shifted Window Multi-Head Self Attention)
- PatchMerging
- 階層計算 (Hierarchical Computation)
- コード例
- 参考文献
Swin Transformerは、Microsoft Researchチームが開発した視覚モデルで、従来のTransformerモデルがコンピュータビジョンタスクにおいて抱える計算複雑性の問題を解決することを目的としています。正式名称は「Shifted Window Transformer」で、階層アーキテクチャとシフトウィンドウメカニズムを導入することで、性能と効率のバランスを実現しています。
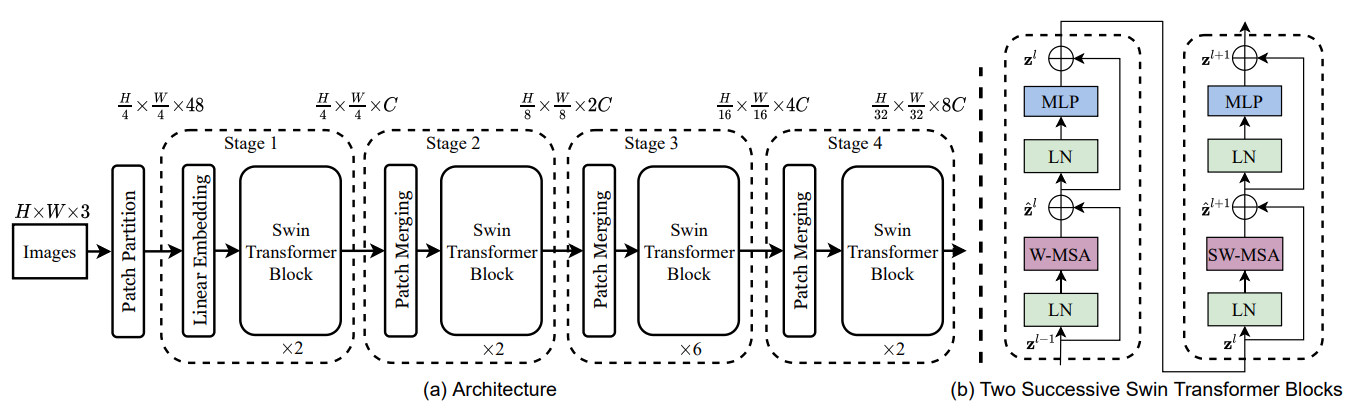
Vision Transformerの課題
- 計算複雑性: 画像データを細かいパッチに分割する必要があり、より多くの特徴を得るためには長いシーケンスを構築する必要があります。自己注意機構の計算複雑性はであり、高解像度画像を処理する際に急速に増加します。
- 局所特徴の捕捉: 画像の視覚情報は多くの場合局所的な関係に依存していますが、標準的なVision Transformerはグローバルな関係を処理するため、局所特徴を効果的に捉えることができません。
Swin Transformerの解決策
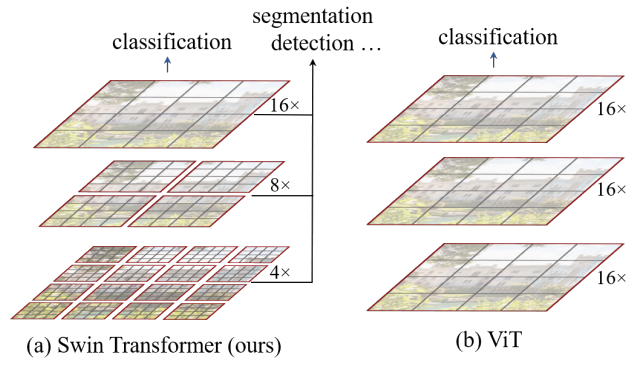
- ウィンドウベースのアプローチ: 長いシーケンスの代わりに、ウィンドウと階層的な形式を採用
- 階層処理:
- 多くのトークンから開始(例:400トークン)
- レイヤーごとにトークンを徐々にマージ(400→200→100トークン)
- トークン数が減少するにつれてウィンドウサイズが増加
- CNNの畳み込みとプーリング操作と同様の概念
Patch Embedding
Patch Embeddingは、入力画像を複数の小さなパッチに分割し、これらのパッチのピクセル値を高次元空間に埋め込むことで、Transformerが処理可能な特徴表現を形成します。
処理手順
- 画像の分割: 入力画像(224×224×3)を小さなパッチに分割
- 畳み込み操作: Conv2d(3, 96, kernel_size=(4, 4), stride=(4, 4))を使用して各パッチを96次元の特徴ベクトルに変換
- カーネルサイズ: 4×4
- ストライド: 4
- 入力チャネル数: 3(RGB画像)
- 出力チャネル数: 96
- 出力サイズの計算: (224 - 4) / 4 + 1 = 56 → 56×56×96の特徴マップを生成
そこで:
kernel_size: 各パッチの空間サイズを決定stride: パッチ間の間隔(ストライド)を決定
特徴と利点
- パッチの表現: 56×56×96の出力は3,136個のパッチを含み、各パッチは96次元のベクトルとして表現される
- パラメータの制御:
- 柔軟な設定: 畳み込みパラメータを変更することで、パッチの数と各パッチの次元を制御可能
ウィンドウ分割 (Window Partition)
Swin Transformerでは、Patch Embeddingで得られた特徴表現に加えて、ウィンドウ分割(Window Partition)によってさらに細分化・処理を行い、ウィンドウ内での局所的アテンションメカニズムにより計算効率を向上させ、局所特徴を捉えることを目的としています。

処理手順と計算
入力: 畳み込み処理後の特徴マップ (56×56×96)
ウィンドウサイズ: 7×7
-
ウィンドウ数の計算:
- 空間次元(高さと幅)におけるウィンドウ分割数: 56 ÷ 7 = 8
- 総ウィンドウ数: 8 × 8 = 64個のウィンドウ
-
分割後の特徴マップ次元: (64, 7, 7, 96)
64: ウィンドウの数 (8×8 = 64個のウィンドウ)7×7: 各ウィンドウの空間次元96: 各ウィンドウ内の特徴チャネル数
Tokenの概念の変化
- 従来のToken: 画像の局所特徴を表し、各Tokenは画像の1つの位置に対応
- ウィンドウ分割後のToken: 各Tokenはウィンドウの内部特徴に対応し、より広範な局所情報を捉える
利点
- 局所構造への注目: モデルが画像の局所構造に集中できる
- 計算量の削減: 各ウィンドウ内でのみアテンション計算を行うため、計算効率が向上
- 情報の捕捉範囲拡大: 元の各空間位置が表す画像情報の一部から、ウィンドウ分割によりより広範な局所情報を捉えることが可能に
W-MSA (Windwow multi-head self attentio)
W-MSA (Window Multi-Head Self Attention) はSwin Transformerの中心的なアテンションメカニズムであり、各ウィンドウ内で独立に自己注意(Self-Attention)を計算することで計算複雑性を削減し、局所特徴を捉えることを目的としています。
入力データ構造
ウィンドウ分割(Window Partition)を経て、特徴マップは以下のようになります:
- ウィンドウ数: 64個
- 各ウィンドウのサイズ: 7×7
- 各位置の特徴チャネル数: 96
- 各ウィンドウの形状: (7, 7, 96)
Multi-Head Self-Attentionの処理手順
-
線形変換:
- 入力特徴行列を3つの異なる行列を用いて線形変換
- 結果としてQuery (Q)、Key (K)、Value (V) を取得
-
マルチヘッド分割:
- ヘッド数: 3個 (例)
- 各ヘッドの入力特徴次元: 96 ÷ 3 = 32次元
- 96次元の入力が3つのヘッドに均等に分割
W-MSAの計算プロセス
各ウィンドウに対して以下の計算を独立に実行:
-
Query, Key, Valueの計算:
- 各ウィンドウ内の49個のピクセル点(7×7)に対してQ, K, Vを計算
-
アテンションスコアの計算:
- : 各ヘッドの次元数 (この例では32)
- : 各位置間の類似性を測定
-
Softmax処理:
- スコアを正規化して確率分布に変換
- 各位置間の相関関係を確率として表現
-
加重和の計算:
- スコアを用いてValue (V) の加重和を計算
- 各位置の最終出力表現を取得
出力の形状
各ヘッドの自己注意計算結果の形状: (64, 3, 49, 49)
64: ウィンドウ数3: ヘッド数49: 各ウィンドウ内の位置数 (7×7)49: 各位置から他の位置へのアテンションスコア (自己アテンション行列)
Window Reverseの目的
Window Reverse操作は、計算された(64, 49, 96)の特徴マップを元の空間次元(56, 56, 96)に復元することを目的としています。
処理手順
-
Reshape操作:
- 各ウィンドウの特徴マップ形状
(49, 96)を(7, 7, 96)に変換 - これにより、各ウィンドウ内の各ピクセル点が96次元の特徴ベクトルを持つ表現になります
- 各ウィンドウの特徴マップ形状
-
ウィンドウの結合:
- 64個のウィンドウを特徴マップ内での位置に従って再配置
- 元の入力特徴マップサイズである56×56に復元
- 64個のウィンドウは8×8のグリッドとして配置
出力結果
復元後の特徴マップ形状: (56, 56, 96)
56×56: 復元された空間次元で、各ピクセル点の位置を表す96: 各ピクセル点の特徴次元で、各位置の特徴情報を表す
SW-MSA (Shifted Window Multi-Head Self Attention)
SW-MSA (Shifted Window Multi-Head Self Attention) は、Swin Transformerのウィンドウ分割とShift操作を組み合わせたアテンションメカニズムです。
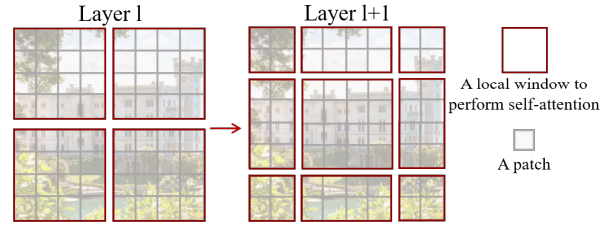
Window MSAの問題点
- 画像を固定ウィンドウ(例: 7×7)に分割し、各ウィンドウ内で自己注意を計算
- 各ウィンドウ内の情報が比較的閉鎖的で、隣接ウィンドウとの情報交換がない
- モデルが各小領域に局限され、ウィンドウ間の関連性を十分に捉えられない
操作の詳細
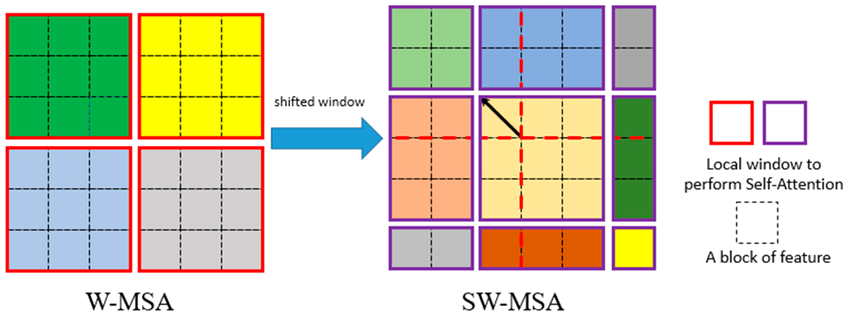
- 初期のウィンドウを4×4のブロックに分割(例: 7×7ウィンドウ)
- 各ブロックで独立した自己注意計算を実行
- シフト時、元の4×4ウィンドウを平移し、9×9の新しいウィンドウに変換
- ウィンドウの重複領域には異なるウィンドウ間の情報が含まれる
利点
- 平移により、モデルはより広範な情報を取得可能
- ウィンドウ間で情報を共有し、特徴を融合することで局所化を回避
SW MSAの問題点
- Shifted Window MSAにより計算量が増加
- ウィンドウスライド後、ウィンドウ数が4×4から9×9に増加し、計算量がほぼ2倍
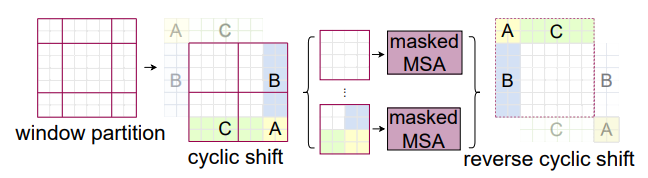
解決策: マスク操作
- マスク操作により不要な計算を削減
- シフト後、ウィンドウ間に重複が生じる
- 重複計算を避けるため、maskを用いて不要な部分を遮蔽
- アテンション計算時、各位置のQとKのマッチングにおいて、softmax使用時に不要な位置の値を負の無限大に設定
- これにより対応位置のアテンション値がゼロに近づき、結果に影響を与えない
出力特徴マップ
SW-MSA後の出力特徴マップ形状: 56×56×96 (入力特徴マップと同一サイズ)
- シフトウィンドウとマスク操作により、元のウィンドウ内自己注意計算を維持しつつ、ウィンドウ間の情報交換と融合を強化
- ウィンドウが移動しても、計算後の特徴は元の位置に戻す必要があり、画像の完全性を保持
PatchMerging
PatchMergingはSwin Transformerにおけるダウンサンプリング操作で、プーリングとは異なり、HとW次元に対してインターリーブサンプリングを行い、その後連結することでH/2、W/2、C*4の特徴マップを生成します。この操作の目的は、計算効率を維持しながら高次元の特徴表現を得るために、入力特徴マップの空間次元(高さと幅)を段階的に縮小し、同時にチャネル数を増加させることです。

特徴と目的
- ダウンサンプリングプロセス: ネットワーク層が深くなるにつれて、特徴マップの空間サイズ(HとW次元)を徐々に縮小
- チャネル数の増加: 空間サイズの縮小と同時にチャネル数(C次元)を増加させ、より複雑な高次情報の捉えを可能にする
- 従来のプーリングとの違い: 隣接するパッチを連結し、連結後の特徴に対して線形変換を行うことでダウンサンプリングを実現
処理手順
入力: H × W × C の特徴マップ
分割と連結 (Splitting and Concatenation)
- 特徴マップを一定のステップサイズ(通常は2)で分割
- 各2×2のパッチをマージ(結合)
- 空間サイズが半分に縮小: H × W → H/2 × W/2
- 各2×2パッチ内の特徴を連結し、新しい特徴次元を生成
- 元のチャネル数Cから連結後のチャネル数4Cに拡張
畳み込み操作
- 連結後の特徴に対して畳み込みを実行し、特徴表現をさらに強化
- 畳み込み操作により特徴空間を変換
- チャネル数が増加しても、畳み込みによりより豊かな特徴が得られる
利点
- 計算効率の維持: プーリングではなく学習可能なパラメータによるダウンサンプリング
- 特徴の豊かさ: 連結と畳み込みにより、局所的な特徴情報を効果的に統合
- 階層的特徴学習: ネットワークが深くなるにつれて、より抽象的で高次の特徴を捉えることが可能
階層計算 (Hierarchical Computation)

Swin Transformerでは、モデルの各層でダウンサンプリング操作を実行し、同時にチャネル数を段階的に増加させます。各層のPatchMerging後の特徴マップは、次の層のAttention計算への入力として使用されます。この方式により、Swin Transformerは計算効率を維持しながら、ますます複雑な特徴を抽出することが可能になります。
処理フロー
-
PatchMerging操作:
- 各層で入力特徴マップに対してダウンサンプリングを実行
- 空間次元(H,W)を縮小し、チャネル次元©を増加
-
特徴マップの伝搬:
- PatchMerging後の特徴マップを次の層の入力として使用
- この特徴マップが次のAttention計算の対象となる
-
線形変換の役割:
- PatchMerging操作では、入力特徴マップを線形変換(通常は畳み込み)により高次元特徴マップに変換
- これにより、後続のアテンション計算により豊富な表現を提供
チャネル数の変化
図から分かる通り、各層でのチャネル数はCから4Cではなく2Cに変化しています。これは以下の理由によるものです:
- 中間の畳み込み層の追加:
- PatchMergingプロセス中に追加の畳み込み層が挿入されている
- この中間層により、チャネル数の増加が段階的に行われる
- 結果として、最終的なチャネル数は4Cではなく2Cとなる
利点
- 計算効率の維持: 階層的なアプローチにより、計算負荷を効果的に管理
- 複雑な特徴の抽出: ネットワークが深くなるにつれて、より抽象的で複雑な特徴を段階的に学習
- 豊富な特徴表現: 各層での線形変換により、後続層に質の高い特徴表現を提供
コード例
PatchEmbed コード例
class PatchEmbed(nn.Module):
"""
2D Image to Patch Embedding
split image into non-overlapping patches 即将图片划分成一个个没有重叠的patch
"""
def __init__(self, patch_size=4, in_c=3, embed_dim=96, norm_layer=None):
super().__init__()
# パッチサイズをタプル形式に変換し、高さと幅の両方に同じ値を適用
patch_size = (patch_size, patch_size)
self.patch_size = patch_size
# 入力チャネル数と埋め込み次元数をクラス属性として保存
self.in_chans = in_c
self.embed_dim = embed_dim
# 畳み込み層を定義: 入力画像をパッチに分割し、指定された次元に埋め込む
# kernel_size = stride により、パッチが重ならないように分割される
self.proj = nn.Conv2d(in_c, embed_dim, kernel_size=patch_size, stride=patch_size)
# 正規化層の設定: 指定されていればその層を使用、なければIdentity(何もしない)
self.norm = norm_layer(embed_dim) if norm_layer else nn.Identity()
def forward(self, x):
# 入力テンソルの形状からバッチサイズ、チャネル数、高さ、幅を取得
_, _, H, W = x.shape
# padding
# 如果输入图片的H,W不是patch_size的整数倍,需要进行padding
# 入力画像の高さまたは幅がパッチサイズの整数倍でない場合、パディングが必要
pad_input = (H % self.patch_size[0] != 0) or (W % self.patch_size[1] != 0)
if pad_input:
# to pad the last 3 dimensions,
# (W_left, W_right, H_top,H_bottom, C_front, C_back)
# 最後の3次元(幅、高さ、チャネル)にパディングを適用
x = F.pad(x, (0, self.patch_size[1] - W % self.patch_size[1], # 表示宽度方向右侧填充数
0, self.patch_size[0] - H % self.patch_size[0], # 表示高度方向底部填充数
0, 0))
# 下采样patch_size倍
# パッチサイズ分だけダウンサンプリングし、パッチへの分割を実行
x = self.proj(x)
_, _, H, W = x.shape
# flatten: [B, C, H, W] -> [B, C, HW]
# transpose: [B, C, HW] -> [B, HW, C]
# テンソルの形状を変更: パッチの系列を1次元に平坦化し、チャネル次元を最後に移動
x = x.flatten(2).transpose(1, 2)
# 正規化層を適用
x = self.norm(x)
# 埋め込み特徴、出力の高さ、出力の幅を返す
return x, H, W
PatchMerging コード例
class PatchMerging(nn.Module):
r""" Patch Merging Layer.
Args:
dim (int): Number of input channels.
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, dim, norm_layer=nn.LayerNorm):
super().__init__()
# 入力チャネル数を保存
self.dim = dim
# 線形変換層を定義: 4*dim次元を2*dim次元に変換(チャネル数を半分に削減)
self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
# 正規化層を定義: 4*dim次元に対して正規化を適用
self.norm = norm_layer(4 * dim)
def forward(self, x, H, W):
"""
x: B, H*W, C
"""
# 入力テンソルの形状を取得
B, L, C = x.shape
# 入力特徴のサイズが正しいか確認(L = H * Wであること)
assert L == H * W, "input feature has wrong size"
# テンソルの形状を[B, H, W, C]に変更し、空間次元を明示的に表現
x = x.view(B, H, W, C)
# padding
# 如果输入feature map的H,W不是2的整数倍,需要进行padding
# 入力feature mapの高さ(H)または幅(W)が2の倍数でない場合、パディングが必要
pad_input = (H % 2 == 1) or (W % 2 == 1)
if pad_input:
# to pad the last 3 dimensions, starting from the last dimension and moving forward.
# (C_front, C_back, W_left, W_right, H_top, H_bottom)
# 注意这里的Tensor通道是[B, H, W, C],所以会和官方文档有些不同
# 最後の3次元(チャネル、幅、高さ)にパディングを適用
# チャネル方向にはパディングなし、幅方向右端にW%2、高さ方向下端にH%2のパディング
x = F.pad(x, (0, 0, 0, W % 2, 0, H % 2))
# 2×2の領域から4つのサブピクセルを抽出
# 高さと幅の偶数番目のインデックスから値を取得(間隔をおいてサンプリング)
x0 = x[:, 0::2, 0::2, :] # [B, H/2, W/2, C] - 左上
x1 = x[:, 1::2, 0::2, :] # [B, H/2, W/2, C] - 左下
x2 = x[:, 0::2, 1::2, :] # [B, H/2, W/2, C] - 右上
x3 = x[:, 1::2, 1::2, :] # [B, H/2, W/2, C] - 右下
# 4つの特徴をチャネル次元(最後の次元)方向に連結
x = torch.cat([x0, x1, x2, x3], -1) # [B, H/2, W/2, 4*C]
# テンソルの形状を[B, H/2*W/2, 4*C]に変更(空間次元を1次元に平坦化)
x = x.view(B, -1, 4 * C) # [B, H/2*W/2, 4*C]
# 正規化層を適用
x = self.norm(x)
# 線形変換を適用し、チャネル数を4*Cから2*Cに削減
x = self.reduction(x) # [B, H/2*W/2, 2*C]
# ダウンサンプリングされた特徴を返す
return x
mask掩码生成とstageスタックのコードモジュール
def create_mask(self, x, H, W):
# SW-MSA用のアテンションマスクを計算
# HpとWpがwindow_sizeの整数倍になるように保証
Hp = int(np.ceil(H / self.window_size)) * self.window_size
Wp = int(np.ceil(W / self.window_size)) * self.window_size
# feature mapと同じチャネル配置順序を持ち、後続のwindow_partitionを容易にする
img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device) # [1, Hp, Wp, 1]
# 高さ方向のスライスを定義:左上(-100)、左中(-100)、左下(-100)の3つの領域
h_slices = (slice(0, -self.window_size), # 0から-window_sizeまで
slice(-self.window_size, -self.shift_size), # -window_sizeから-shift_sizeまで
slice(-self.shift_size, None)) # -shift_sizeから終端まで
# 幅方向のスライスを定義:同様に3つの領域
w_slices = (slice(0, -self.window_size), # 0から-window_sizeまで
slice(-self.window_size, -self.shift_size), # -window_sizeから-shift_sizeまで
slice(-self.shift_size, None)) # -shift_sizeから終端まで
cnt = 0
# 3x3の領域(合計9領域)それぞれに異なる番号を割り当てる
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt # 各領域に0〜8の番号を割り当て
cnt += 1
# img_maskを個別のウィンドウに分割
mask_windows = window_partition(img_mask, self.window_size) # [nW, Mh, Mw, 1]
# 各ウィンドウを1次元に平坦化
mask_windows = mask_windows.view(-1, self.window_size * self.window_size) # [nW, Mh*Mw]
# アテンションマスクの計算:ブロードキャストメカニズムを使用
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2) # [nW, 1, Mh*Mw] - [nW, Mh*Mw, 1]
# [nW, Mh*Mw, Mh*Mw] - 各ウィンドウ内の位置間の関係を表す
# 自己アテンションメカニズムを求める必要があるため、同じ領域は0で表し、異なる領域は-100で埋める
# 0でない位置には-100を、0の位置には0を設定
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
return attn_mask
# 4. stageスタック部分コード:
class BasicLayer(nn.Module):
"""
1つのステージ用の基本的なSwin Transformerレイヤー
Args:
dim (int): 入力チャネル数
depth (int): ブロック数
num_heads (int): アテンションヘッド数
window_size (int): ローカルウィンドウサイズ
mlp_ratio (float): MLP隠れ次元と埋め込み次元の比率
qkv_bias (bool, optional): Trueの場合、query, key, valueに学習可能なバイアスを追加
drop (float, optional): ドロップアウト率
attn_drop (float, optional): アテンションドロップアウト率
drop_path (float | tuple[float], optional): 確率的深度率
norm_layer (nn.Module, optional): 正規化層
downsample (nn.Module | None, optional): レイヤー終端のダウンサンプル層
use_checkpoint (bool): メモリ節約のためのチェックポイント使用有無
"""
def __init__(self, dim, depth, num_heads, window_size,
mlp_ratio=4., qkv_bias=True, drop=0., attn_drop=0.,
drop_path=0., norm_layer=nn.LayerNorm, downsample=None, use_checkpoint=False):
super().__init__()
self.dim = dim
self.depth = depth # このレイヤー内のブロック数
self.window_size = window_size
self.use_checkpoint = use_checkpoint
self.shift_size = window_size // 2 # 右および下方向へのシフトサイズ(ウィンドウサイズの半分)
# ブロックの構築
self.blocks = nn.ModuleList([
SwinTransformerBlock(
dim=dim,
num_heads=num_heads,
window_size=window_size,
# シフトサイズが0かどうかでW-MSAかSW-MSAかを決定
shift_size=0 if (i % 2 == 0) else self.shift_size,
mlp_ratio=mlp_ratio,
qkv_bias=qkv_bias,
drop=drop,
attn_drop=attn_drop,
# ドロップパス率をリスト形式か単一値で設定
drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
norm_layer=norm_layer)
for i in range(depth)]) # depth数分のSwinTransformerBlockを生成
# パッチマージング層(PatchMergingクラス)
if downsample is not None:
self.downsample = downsample(dim=dim, norm_layer=norm_layer)
else:
self.downsample = None
def create_mask(self, x, H, W):
# SW-MSA用のアテンションマスクを計算(前述のcreate_mask関数と同じ内容)
def forward(self, x, H, W):
# maskマスクの作成
attn_mask = self.create_mask(x, H, W) # [nW, Mh*Mw, Mh*Mw]
# 各ブロックに対して順伝播
for blk in self.blocks:
blk.H, blk.W = H, W # ブロックに高さと幅の情報を設定
# ジットコンパイル中でなく、チェックポイント使用の場合はメモリ節約モード
if not torch.jit.is_scripting() and self.use_checkpoint:
x = checkpoint.checkpoint(blk, x, attn_mask)
else:
x = blk(x, attn_mask) # 通常の順伝播
# ダウンサンプル層がある場合、適用する
if self.downsample is not None:
x = self.downsample(x, H, W)
# 高さと幅を更新((H+1)//2と(W+1)//2により、奇数の場合も適切に処理)
H, W = (H + 1) // 2, (W + 1) // 2
# 処理後の特徴、高さ、幅を返す
return x, H, W
SW-MSAの計算
class SwinTransformerBlock(nn.Module):
r""" Swin Transformer Block.
Args:
dim (int): 入力チャネル数
num_heads (int): アテンションヘッド数
window_size (int): ウィンドウサイズ
shift_size (int): SW-MSA用のシフトサイズ
mlp_ratio (float): MLP隠れ次元と埋め込み次元の比率
qkv_bias (bool, optional): Trueの場合、query, key, valueに学習可能なバイアスを追加
drop (float, optional): ドロップアウト率
attn_drop (float, optional): アテンションドロップアウト率
drop_path (float, optional): 確率的深度率
act_layer (nn.Module, optional): 活性化層
norm_layer (nn.Module, optional): 正規化層
"""
def __init__(self, dim, num_heads, window_size=7, shift_size=0,
mlp_ratio=4., qkv_bias=True, drop=0., attn_drop=0., drop_path=0.,
act_layer=nn.GELU, norm_layer=nn.LayerNorm):
super().__init__()
# 各パラメータをクラス属性として保存
self.dim = dim
self.num_heads = num_heads
self.window_size = window_size
self.shift_size = shift_size
self.mlp_ratio = mlp_ratio
# シフトサイズが0〜window_sizeの範囲内にあることを確認
assert 0 <= self.shift_size < self.window_size, "shift_size must in 0-window_size"
# 最初の正規化層
self.norm1 = norm_layer(dim)
# ウィンドウアテンション層
self.attn = WindowAttention(
dim, window_size=(self.window_size, self.window_size), num_heads=num_heads, qkv_bias=qkv_bias,
attn_drop=attn_drop, proj_drop=drop)
# ドロップパス層(drop_pathが0より大きい場合のみ適用)
self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
# 2番目の正規化層
self.norm2 = norm_layer(dim)
# MLP層の隠れ次元数を計算
mlp_hidden_dim = int(dim * mlp_ratio)
# MLP層の定義
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)
def forward(self, x, attn_mask):
# 高さと幅をクラス属性から取得
H, W = self.H, self.W
# 入力テンソルの形状を取得
B, L, C = x.shape
# 入力特徴のサイズが正しいか確認
assert L == H * W, "input feature has wrong size"
# ショートカット接続用に元の入力を保存
shortcut = x
# 最初の正規化を適用
x = self.norm1(x)
# テンソルの形状を[B, H, W, C]に変更
x = x.view(B, H, W, C)
# pad feature maps to multiples of window size
# feature mapをwindow sizeの整数倍にパディング
# パディング量を計算(左、上、右、下)
pad_l = pad_t = 0 # 左と上のパディングは0
pad_r = (self.window_size - W % self.window_size) % self.window_size # 右のパディング量
pad_b = (self.window_size - H % self.window_size) % self.window_size # 下のパディング量
# パディングを適用
x = F.pad(x, (0, 0, pad_t, pad_b, pad_l, pad_r))
# パディング後の高さと幅を取得
_, Hp, Wp, _ = x.shape
# cyclic shift(循環シフト)
if self.shift_size > 0:
# paper中、滑动的size是窗口大小的/2(向下取整)
# torch.rollはH,Wの次元を例にすると、負値は左上に移動、正值は右下に移動
# 溢れた値は対角方向に出現する(循環移動)
shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
else:
shifted_x = x
attn_mask = None # シフトがない場合はアテンションマスクをNoneに
# partition windows(ウィンドウ分割)
# シフトされた特徴をウィンドウに分割
x_windows = window_partition(shifted_x, self.window_size) # [nW*B, Mh, Mw, C]
# ウィンドウを1次元に平坦化
x_windows = x_windows.view(-1, self.window_size * self.window_size, C) # [nW*B, Mh*Mw, C]
# W-MSA/SW-MSA(ウィンドウマルチヘッドセルフアテンション)
# アテンション計算を実行
attn_windows = self.attn(x_windows, mask=attn_mask) # [nW*B, Mh*Mw, C]
# merge windows(ウィンドウ結合)
# アテンション結果をウィンドウ形状に戻す
attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C) # [nW*B, Mh, Mw, C]
# ウィンドウを元の特徴マップ形状に復元
shifted_x = window_reverse(attn_windows, self.window_size, Hp, Wp) # [B, H', W', C]
# reverse cyclic shift(逆循環シフト)
if self.shift_size > 0:
# シフトを元に戻す
x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
else:
x = shifted_x
# パディングしたデータを削除
if pad_r > 0 or pad_b > 0:
# 前にパディングしたデータを除去
x = x[:, :H, :W, :].contiguous()
# テンソルの形状を[B, H*W, C]に戻す
x = x.view(B, H * W, C)
# FFN(フィードフォワードネットワーク)
# ショートカット接続とドロップパスを適用
x = shortcut + self.drop_path(x)
# 2番目のショートカット接続とMLPを適用
x = x + self.drop_path(self.mlp(self.norm2(x)))
# 処理後の特徴を返す
return x
