Vision Transformer(ViT)

2024/4/10 AI Deep Learning 機械学習 AI 人工知能深層学習画像認識画像分類 image classification transformer ViT

Vision Transformer (ViT)

ViTはTransformerアーキテクチャを画像認識に応用したもので、パッチ単位で画像を処理します。

ViT

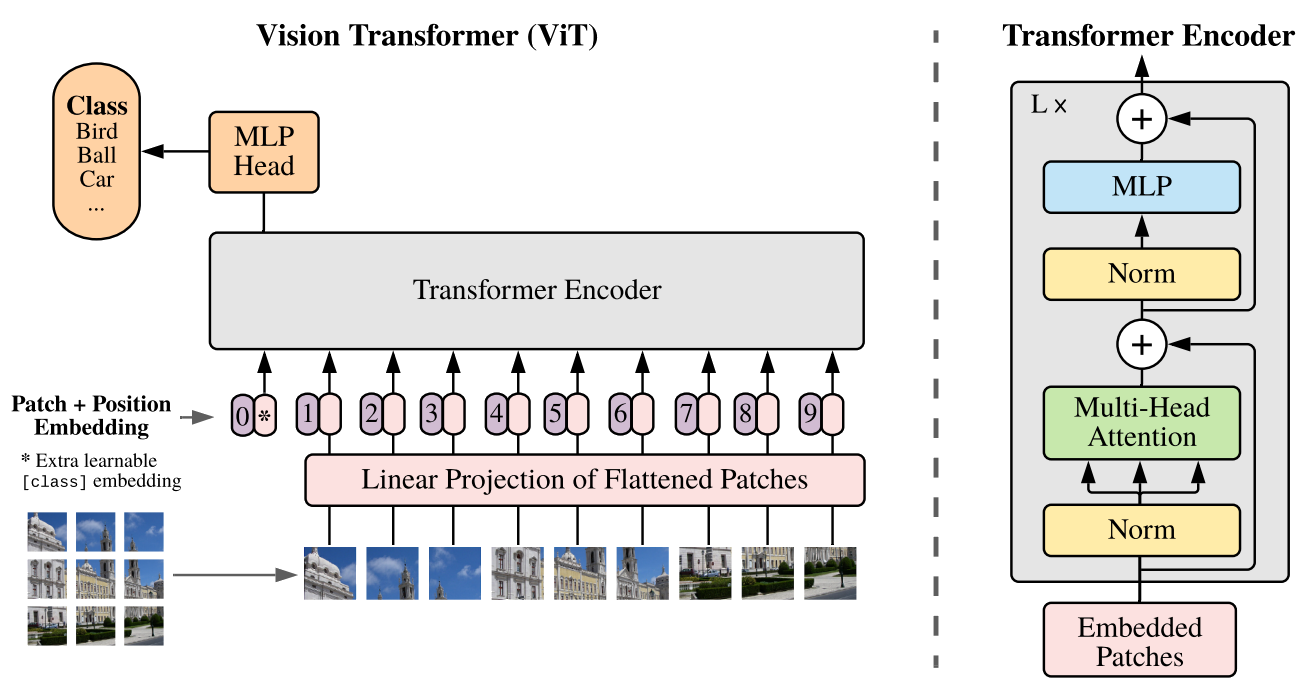
画像のパッチ化（Patch）

入力画像（例：224×224×3）を固定サイズのパッチに分割。
例: 16×16×3 のパッチに分割 → 合計196個のパッチ（14×14）。
各パッチを768次元のベクトルに変換（=> Token）。

Position Embedding

自然言語処理（NLP）において、Transformerなどのモデルは入力されたトークン列を順序なしの集合として扱います。しかし、言語には「単語の並び順」が意味を左右するという重要な性質があります。

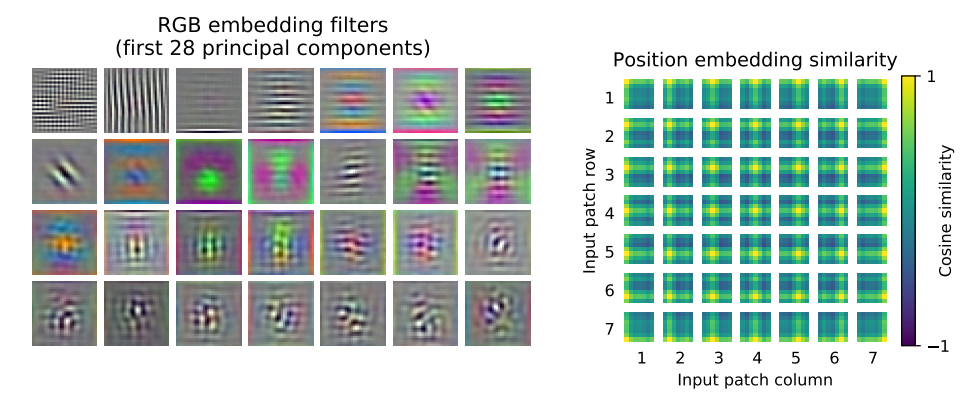
position embedding

ViT（Vision Transformer）におけるposition embeddingの目的は、画像を複数のパッチ（小さな領域）に分割して処理する際に、各パッチが画像内で持つ空間的な位置情報をモデルに与えることです。Transformerアーキテクチャは入力データの順序情報を持たないため、この位置情報を明示的に追加しないと、どのパッチがどこにあるかという空間構造に関する重要な情報が失われてしまいます。

ViTでは、自然言語処理で使われるTransformerと同様に、sin/cos関数によるposition embeddingを用いて、各パッチに位置情報を埋め込みます。

数式

位置 pos、次元 i に対して、

$ PE(\text{pos},\ 2i) = \sin\left( \frac{\text{pos}}{10000^{2i / d_{\text{model}}}} \right) $ $ PE(\text{pos},\ 2i+1) = \cos\left( \frac{\text{pos}}{10000^{2i / d_{\text{model}}}} \right) $

pos: トークンまたはパッチの位置（0, 1, 2,…）
i: 埋め込みベクトルの次元（0 ≤ i < d_model/2）
d_model: 入力ベクトルの次元（例: 768）

コード例

'''Attention Is All You Need'''

class Positional_Encoding(nn.Module):
    def __init__(self, embed, pad_size, dropout, device):
        super(Positional_Encoding, self).__init__()
        self.device = device
        self.pe = torch.tensor([[pos / (10000.0 ** (i // 2 * 2.0 / embed)) for i in range(embed)] for pos in range(pad_size)])
        self.pe[:, 0::2] = np.sin(self.pe[:, 0::2])
        self.pe[:, 1::2] = np.cos(self.pe[:, 1::2])
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        out = x + nn.Parameter(self.pe, requires_grad=False).to(self.device)
        out = self.dropout(out)
        return out


class Model(nn.Module):
    def __init__(self, config):
        ... ...
        self.postion_embedding = Positional_Encoding(self.dim_model, config.pad_num, config.dropout, config.device)
        ... ...

    def forward(self, x):
        out = self.postion_embedding(x)
        ... ...

cls token

ViT（Vision Transformer）におけるトークンの目的は、画像全体の意味的な情報を集約して分類タスクに利用することです。

cls

Transformerでは各パッチが局所的な特徴を表す一方で、グローバルな情報や画像全体の文脈を直接捉えることは困難です。この問題を解決するために、ViTでは入力される各画像パッチの先頭に特別なトークンであるトークンを追加します。このトークンは、Transformer内部での自己注意機構（Self-Attention）を通じて、他のすべてのパッチトークンからの情報を収集し、最終的に画像全体を表現する特徴ベクトルとなります。分類時には、このトークンに対応する出力を分類ヘッド（通常は全結合層）に入力することで、画像のカテゴリを予測します。

Encoder

ViTにTransformerのEncoder層を利用しが、画像分類任務には特徴の理解であるから、Decoder層は省略します。以下の図は、ViTのEncoder層を示したものです。

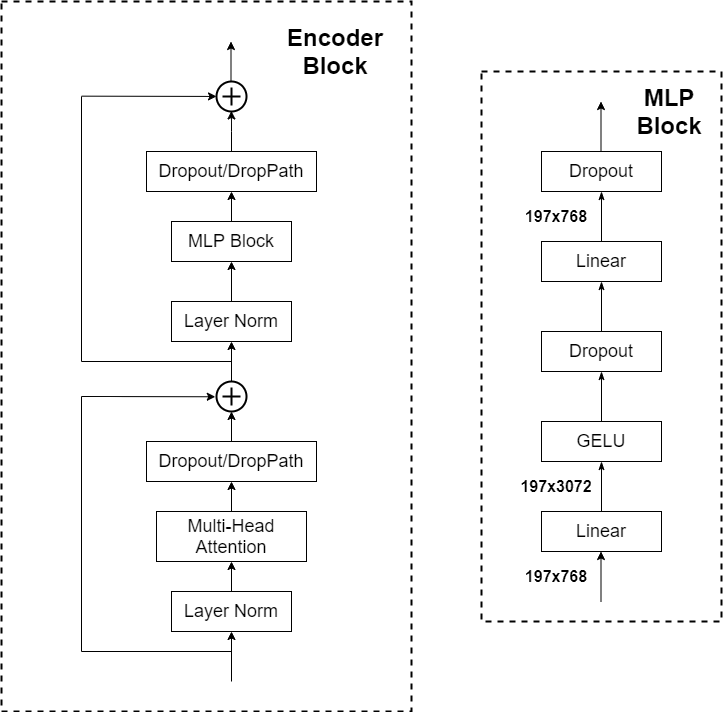
ViT Encoder

以下の図は、TransformerのEncoderとDecoderを示したものです。

Transformer Encoder

この二つの図を比べて、ViTのEncoderは、TransformerのEncoderMulti-Head Attention / Feed Forward Network後Normalizationの流れと異なって、まずはLayer Normalization、次にMulti-Head Attention / Feed Forward Networkを行うと示しています。

ViTで画像処理の流れ

画像を16×16などのサイズで分割 → パッチ化
各パッチを線形変換して埋め込みベクトルに
<cls>トークンを追加（分類用）
Position Embeddingを各Tokenに加算
Transformer Encoderへ入力

CNNにかえりみる

平移等価性（Translation Equivariance）

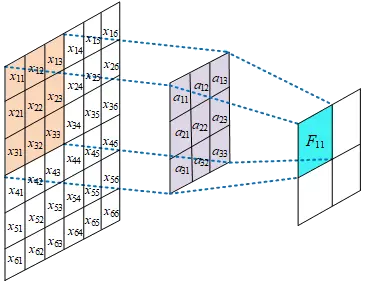
CNN weight shares

畳み込みは「窓関数」のように画像上をスライドしながら演算を行います。
平移等価性とは、画像全体を平行移動させた場合でも、その特徴マップも同じように平行移動するという性質です。

数式

数学的に表現すると：

$ f(g(x)) = g(f(x)) $

f：畳み込み操作
g：平行移動操作

利点

この性質により、物体が画像内のどこにあっても、その特徴を一貫して検出できます。
並列計算が容易で、GPUなどのハードウェアを活用して高速化が可能です。

局所性（Locality）

畳み込みカーネルは通常3×3などの小さなサイズを使い、画像の局所的な領域のみを観測します。
局所性があることで、隣接するピクセル間の関係性を強調し、エッジやテクスチャなどの局所的特徴を効果的に抽出できます。

利点

隣接する画素が意味的に関連していることが多いという前提に基づいており、自然画像の構造に適しています。

帰納的バイアス

帰納的バイアス（Inductive Bias）とは、モデルが持つ仮定や先験知識のことです。これにより、特定のタスクに対してより効率的に学習できるようになります。

CNNにおける帰納的バイアス

帰納的バイアスとは、モデルが持つ仮定や先験知識のことです。これにより、特定のタスクに対してより効率的に学習できるようになります。

主なバイアス

空間的局所性 (Spatial Locality)
- 画像では近い位置にあるピクセルが相互に関係していると考えます。
- 例: 太陽と空はよく一緒に現れます。
平移等価性 (Translation Equivariance)
- 物体が画像内で移動しても、それが特徴マップ上で同様に移動することを保証します。
- 例: 左上にあった太陽が右上に移動しても、畳み込み結果も同様に移動します。

これらのバイアスにより、CNNは画像認識において非常に効果的なモデルとなっています。

ViTの特徴と実め

入力画像を固定サイズのパッチに分割し、それぞれをベクトルとして扱います。
Attention機構によって、すべてのパッチ間の関係性を同時に考慮できます。

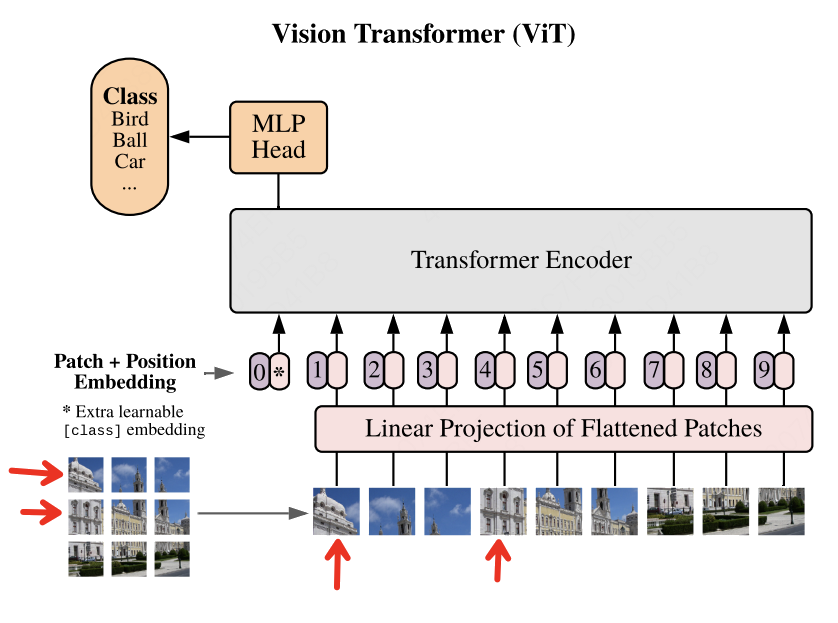
ViT bias

図中の矢印で示された2つの部分は、同じ建物の一部です。CNN（畳み込みニューロンネットワーク）では、適切なサイズの畳み込みカーネルを使えば、これらの領域を一緒に捉えることができます。しかし、ViT（Vision Transformer）では、これらのパッチ間の位置が遠く離されてしまい、さらにパッチを細かく分割すると、その距離はより一層広がってしまいます。Attention機構によってベクトル間の関係性を学ぶことは可能ですが、空間的な局所性という点では、ViTはCNNほど優れていないと言えます。

また、「平移等価性」に注目すると、ViTは各パッチの位置情報を学習する必要があるため、同じ内容のパッチでも場所が変わると出力結果も変わってしまうという問題があります。このように、ViTは画像認識における「帰納的バイアス（inductive bias）」の仮定をうまく維持できていないとも言えます。

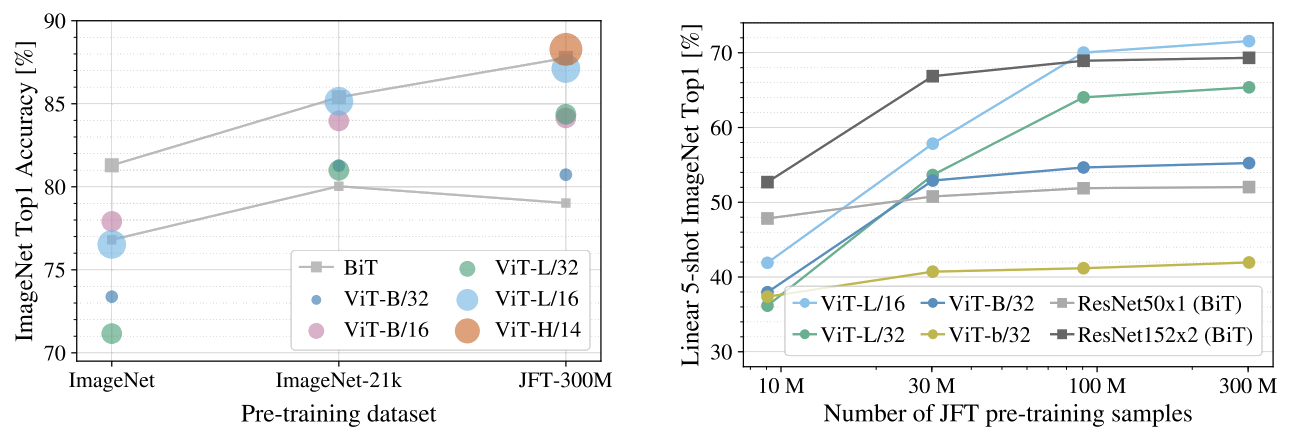
ViT samples acc

異なるサイズのデータセットでの事前学習

ImageNet（約140万枚）、ImageNet-21k（約1400万枚）、JFT-300M（約3億枚）でViTを事前学習させた結果、データ量が少ないImageNetではViT-LargeはResNet系のBiTに劣るが、データ量が多くなるにつれてViTの性能が向上し、最終的にBiTを上回ることが確認されています。
このことから、「ViTは画像における局所性や平移等価性といった帰納的バイアスを持たないが、大量のデータがあれば、それらをAttention機構を通じて学ぶことができる」という結論が導かれます。
サブセットを使ったFew-shot実験

JFT-300Mからランダムに抽出した9M、30M、90Mなどの部分集合で学習を行い、正則化なし・ハイパーパラメータ固定の条件下で評価しました。結果として、ViTは小規模データではResNetよりも過学習が起きやすく性能も低いですが、データ量が増えるとResNetを上回る性能を発揮します。

これは「畳み込みによる帰納的バイアスは小規模データでは有効だが、大規模データではむしろ制約となり得る」という重要な知見を示しています。Transformer系のモデルには有名な特徴があります。「データがあれば、何とかなる」 つまり、十分な量の学習データがあれば、ViTはピクセル単位の関係性を十分に学習し、帰納的バイアスの問題を解消することができます。

要するに、「ViTは少ないデータでは弱いが、データが多ければ驚くべき力を発揮する」ということです。

LOADING