LOADING

読み込みが遅い場合はキャッシュを有効にしてください。ブラウザはデフォルトで有効になっています

StyleGANシリーズ(v1~v3)の画像生成技術

2024/4/8 AI Deep Learning PyTorch Python 機械学習 AI 人工知能 深層学習 生成AI 画像生成

目次

AdaIN（自適応インスタンス正規化）

  • AdaIN は、スタイル転送を任意のスタイル画像に対してリアルタイムで実行できるようにする手法です。

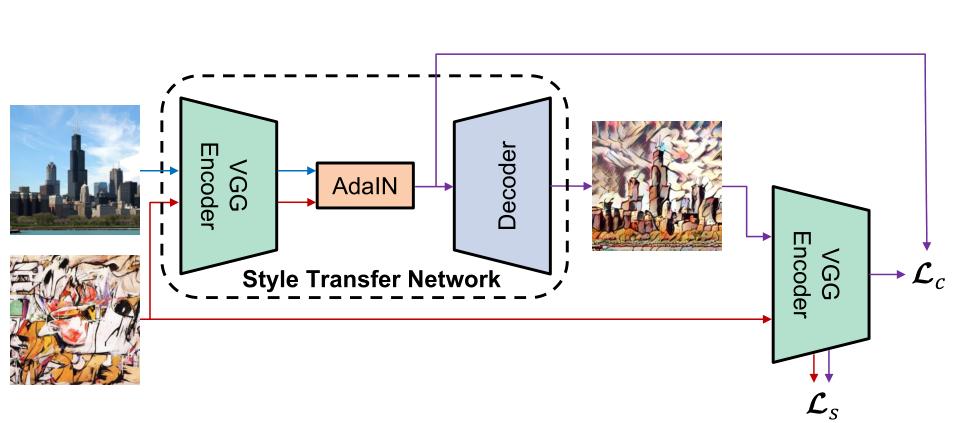
AdaIN

  • 中核的なアイデアは、内容画像の特徴統計量（平均と標準偏差）をスタイル画像のそれらに合わせることで、スタイル情報を効果的に伝達することです。
  • リアルタイムかつ任意のスタイル画像を用いたスタイル転送を実現する非常に柔軟で効率的な手法です。
  • 学習不要のアフィン変換と簡単なネットワーク構造により、高い表現力と汎用性を持ちます。

数式による定義

$ AdaIN(x, y) = \sigma(y) \left( \frac{x - \mu(x)}{\sigma(x)} \right) + \mu(y) $
  • $x$：内容画像の特徴マップ
  • $y$：スタイル画像の特徴マップ
  • $μ(x)$、$σ(x)$：内容画像の各チャネルにおける平均と標準偏差
  • $μ(y)$、$σ(y)$：スタイル画像の各チャネルにおける平均と標準偏差

特徴

  1. 固定されたスタイル制約なし：
    • 既存のスタイル転送モデルは特定のスタイルセットに限定されるが、AdaIN は任意のスタイル画像を扱える。
  2. ユーザー制御の柔軟性：
    • 内容とスタイルのバランス調整、スタイル間補間、色や空間制御などの高度な編集が可能。
  3. 高速処理：
    • 最速のスタイル転送手法と同等の速度を持つ。
  4. 学習可能なパラメータなし：
    • BatchNorm や InstanceNorm のように学習対象のアフィン変換パラメータがない。代わりにスタイル画像から直接パラメータを計算する。

ネットワーク構造

  • エンコーダー-デコーダー構造を使用：
    • エンコーダー：事前に学習済みの VGG-19 を使用して内容画像とスタイル画像を特徴空間に変換。
    • AdaIN 層：内容特徴とスタイル特徴を組み合わせて新しい特徴マップ t を生成：
      $ t = AdaIN(f(c), f(s)) $
    • デコーダー：特徴マップ t を画像空間に戻し、スタイル化された画像を出力：
      $ T(c, s) = g(t) $

損失関数

  • コンテンツ損失 $ L_c $:
    • 入力特徴マップと再構成された特徴マップの差分を最小化：
    $ L_c = \| f(g(t)) - t \|_2 $
  • スタイル損失 $ L_s $:
    • スタイル画像と生成画像の各層における平均・標準偏差の差分を最小化：
    $ L_s = \sum_{i=1}^L \|\mu(\phi_i(g(t))) - \mu(\phi_i(g(s)))\|_2 + \sum_{i=1}^L \|\sigma(\phi_i(g(t))) - \sigma(\phi_i(g(s)))\|_2 $

StyleGAN v1

概要

  • StyleGAN v1 は、NVIDIA によって 2018 年に提案された生成敵ネットワーク（GAN）のアーキテクチャです。
  • 主な目的は、高解像度かつ詳細な顔画像の生成と、画像の視覚的特徴をより細かく制御可能にすること。
  • 基盤は ProGAN の漸進的訓練法（progressive growing）に基づいていますが、スタイルベースの生成器を導入することで、画像生成における柔軟性と制御性が大きく向上しています。

アーキテクチャの主な特徴

デュアルネットワーク構造

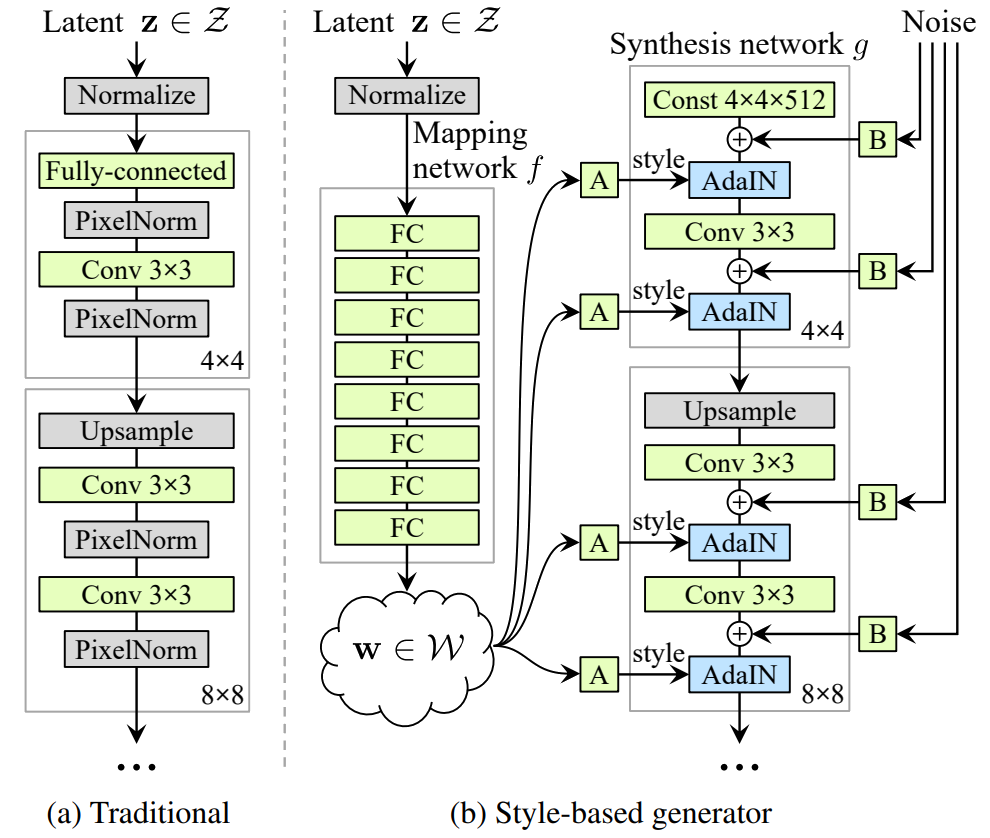
StyleGAN

  • マッピングネットワーク (Mapping Network):

    • 入力潜在コード z を中間潜在空間 w へ変換。
    • z は事前分布（通常ガウス分布）に従うが、w はデータ分布に依存しないので、より良い特徴分離（解釈可能な表現）が得られる。
    • マッピング関数 f: z → w は 8 層の全結合ネットワークで構成される。

  • 合成ネットワーク (Synthesis Network):

    • 学習可能な定数テンソルから出発し、各層で AdaIN を使ってスタイル情報を注入。
    • 各レイヤーで w が異なる視覚的特徴（顔の形、髪色、目・鼻・口の形状など）を制御する。
    • 最終的に 1024×1024 解像度の画像を生成。

スタイルベースの生成器 (Style-based Generator)

  • AdaIN 層を使用して、画像生成中にスタイル情報を注入：
    $ \text{AdaIN}(x, y) = y_{\text{scale}} \cdot \frac{x - \mu(x)}{\sigma(x)} + y_{\text{shift}} $
    - `y_scale`, `y_shift` は中間潜在コード `w` から学習されたアフィン変換パラメータ。 - 各畳み込み層で `w` を適用することで、**局所的なスタイル調整**が可能。

ランダムノイズの導入（Stochastic Variation）

  • 各解像度レベルで Gaussian ノイズを追加。
  • 髪の毛やほくろなどの微細なランダム性を再現。
  • ノイズ係数は各層ごとに学習可能で、特定の特徴に影響を与えずに多様性を持たせることができる。

訓練方法と損失関数

  • Progressive Growing:
    • ProGAN と同様に、低解像度（4×4）から始めて、段階的に解像度を上げながらネットワークを拡張しながら訓練。
  • 非条件 GAN:
    • クラスラベルなどの条件情報なしで訓練。
    • ただし、スタイルコード w を手動で編集することで、任意の属性を調整可能。

FID（Fréchet Inception Distance）

  • FID は、GAN の生成画像品質を評価するための指標で、値が小さいほど高品質な画像が生成されていることを示します。
  • 真の画像と生成画像の特徴空間における統計的距離を測定することで、視覚的な類似性を数値化しています。
  • Inception V3 は分顔識別用に訓練されているが、FIDではクラス分類能力ではなく、画像の構造や多様性を捉える特徴抽出器として利用されます。
  • 特徴空間上での分布の近さ（平均と分散の一致度）を測定することで、生成画像がどれだけ現実的な分布に近づいているかを評価できます。
  • この指標は生成モデルの目的に合致しており、視覚的に自然な画像が得られているかどうかを客観的に比較可能です。

計算方法

  1. Inception V3 を使用して特徴抽出

    • ImageNet で事前学習済みの Inception V3 モデルを使用。
    • 全結合層（最終出力層）の前の 2048次元の特徴ベクトル を抽出。

  2. 真の画像集合と生成画像集合の特徴分布を比較

    • 各画像の特徴ベクトルから、以下の統計量を計算：
      • $μ_r$：真の画像の平均
      • $μ_g$：生成画像の平均
      • $Σ_r$：真の画像の共分散行列
      • $Σ_g$：生成画像の共分散行列

  3. FIDスコアの計算公式

    $ \text{FID} = \| \mu_r - \mu_g \|^2 + \text{Tr}(\Sigma_r + \Sigma_g - 2 (\Sigma_r \Sigma_g)^{1/2}) $
    • $Tr$：トレース（行列の対角成分の和）
    • $(\Sigma_r \Sigma_g)^{1/2}$：行列の幾何平均

二つの量化解離度（Latent Space Disentanglement）の方法

  • 解離（disentanglement）とは：潜在空間内の各次元が、画像の個別の視覚的変化因子（例：性別、髪色、年齢など）に対応している状態。
  • 従来の潜在空間 Z では、事前分布に従う必要があるため、特徴が絡み合っている（entangled）傾向がある。
  • 中間潜在空間 W は、マッピングネットワークによって自由に学習されるため、より線形かつ解離的な表現が期待できる。

しかし、これを定量的に評価する手段が必要であり、以下の2つの新しいメトリクスが提案されました：

感知パス長（Perceptual Path Length）

  • 隠れベクトルを線形補間すると、生成画像に非線形な変化が現れることがある。
  • これは、潜在空間が非線形・絡み合った構造を持っていることを示唆する。
  • よって、補間時の画像の変化の滑らかさを測定することで、潜在空間の解離度が評価できる。
計算方法
  • 任意の2点 $z_1$, $z_1$ を選んで球面補間（slerp）を行う。
  • 各ステップ $t$ に対して、$G(slerp(z_1, z_2; t))$ を生成し、隣接する画像の知覚距離を累積してパス長を計算する。
  • 知覚距離 $d(x, y)$ は、VGG16 の中間特徴との差分で算出。
数式
$ l_W = \mathbb{E}\left[ \frac{1}{\epsilon^2} d\left(G(\text{slerp}(z_1, z_2; t)), G(\text{slerp}(z_1, z_2; t + \epsilon))\right)\right] $
  • $W$ 空間では、$w_1 = f(z_1)$, $w_2 = f(z_2)$ として線形補間（lerp）を使用。
解釈
  • 値が小さいほど滑らかな遷移 → 解離されている。
  • FID スコアとともに減少すれば、高品質な画像＋解離性の向上を裏付ける証拠となる。

線形可分性（Linear Separability）

  • 完全に解離された潜在空間であれば、特定の属性に対応する方向ベクトルが存在するはず。
  • 例えば、「性別」ならその方向に沿って進むことで「男→女」への変化が得られる。
  • このような超平面による分離の容易さから、潜在空間の解離度を評価可能。
計算手順

  1. 40種類の属性分類器の訓練

    • CelebA-HQ データセットを使って、40の二値属性（例：男性/女性、笑顔/無表情）に対する判別器を訓練。
    • 判別器構造は StyleGAN の判別器と同じ。

  2. 100,000枚の画像生成と分類

    • 生成器 G で大量の画像を生成し、分類器で属性を予測。
    • 分類結果の信頼度に基づき、50%の低信頼データを除去。

  3. 線形SVMによる分離

    • 各属性に対して、潜在空間 Z または W 上に線形 SVM をフィット。
    • SVM の超平面により、潜在コードを分類。

  4. 条件エントロピーで性能評価

    • SVM の予測ラベル X と、分類器の真ラベル Y の間の条件エントロピー H(Y|X) を計算。
    • 小さいほど、超平面で正確に分離できている → 解離が高い。
最終評価値
$ \exp\left( \sum_i H(Y_i | X_i) \right) $
- 対数領域からの変換（指数関数）により、直感的な比較が可能。

対比

指標名 特徴 解釈
感知パス長 補間時の画像変化の滑らかさを測定 値が小さいほど解離されている
線形可分性 SVMによる属性分離能力を測定 値が小さいほど解離されている

StyleGAN v2

  • StyleGAN v1 では、生成画像に「水滴状のアーティファクト（water-drop artifacts）」が発生することが確認された。
  • この問題は視覚的には目立たない場合もあるが、ネットワーク内部の活性化を見ると常に存在しており、品質向上の妨げになっていた。

AdaIN の置き換え：Modulation + Demodulation

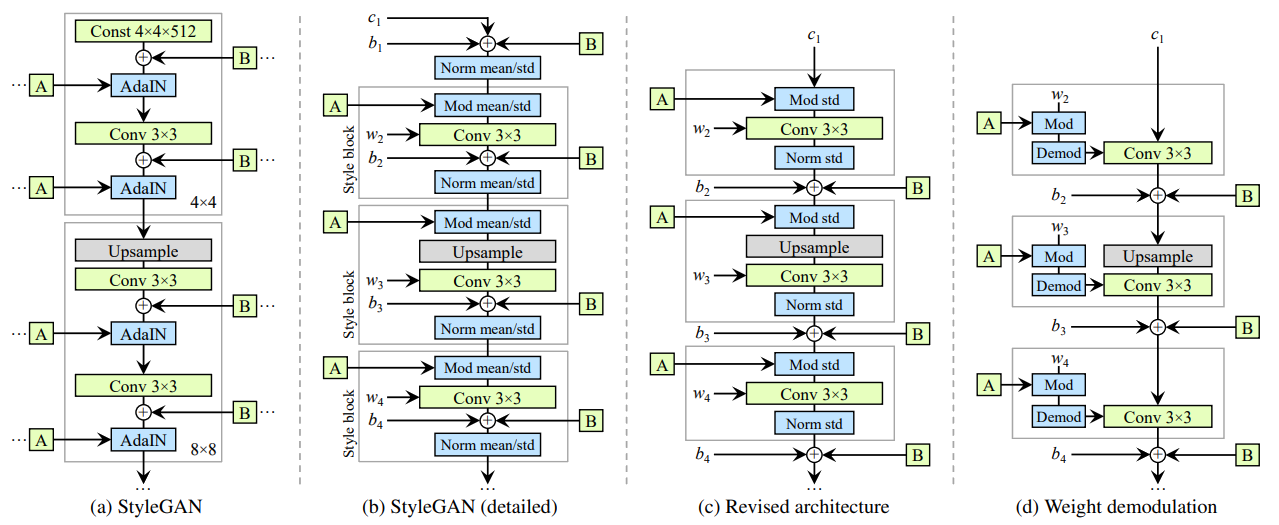
stylegan_v2

概念 説明
変更前 (StyleGAN v1) AdaIN を使用して、特徴マップの平均と標準偏差を正規化し、スタイル情報を注入。
変更後 (StyleGAN v2) AdaIN を分解し、代わりに 重みの調製 (modulation) と解調 (demodulation) を導入。

改良のポイント：

  1. 偏り (bias) とノイズの移動

    • ノイズ加算やバイアスの適用を、AdaIN 層の外側に移動。
    • スタイルに依存しない部分を分離し、より予測可能な挙動を実現。

  2. 平均値の除去

    • 平均値の正規化を廃止し、標準偏差のみで特徴調整を行う。
    • これにより、特徴間の相対的な情報損失を防ぐ。

  3. モジュールの内聚性向上

    • 各層の処理が独立性を持ち、構造が簡潔かつ明確に。
    • モジュール間の結合度が低下し、保守性・拡張性が向上。

数式による表現

重みの調製（Modulation）

$ w'_{ijk} = w_{ijk} \cdot s_i $
  • $w$: 元の重み
  • $s_i$: 第 i 番目の入力特徴マップに対応するスケーリング係数（中間潜在コード $w$ から得られる）
  • $j$, $k$: 出力チャネルと空間カーネル位置

解調（Demodulation）

$ w'_{ijk} = \frac{w'_{ijk}}{\sqrt{\sum_{j,k} (w'_{ijk})^2 + \epsilon}} $
  • 各出力チャネルに対して L2 正規化を行い、勾配爆発を防止。
  • $\epsilon$: ゼロ除算回避用の小さな定数。

FID・P&R の限界と PPL の重要性

  • FID と Precision/Recall (P&R) は一般的な指標だが、画像の細部品質まで正確には反映できない。
  • 同じ FID/P&R 値でも、画像の質に差が出るケースが存在。

PPL（Perceptual Path Length）の役割

  • 隠れ空間における微小変化に対する画像変化の滑らかさを測定。
  • 低い PPL 値は、隠れ空間と画像空間のマッピングが滑らかであることを示唆。
  • 画像品質と強い相関があることが実証された。

正則化手法の導入

路径長正則化（Path Length Regularization）

  • 目的: 隠れ空間と画像空間の写像を滑らかに保つことで、訓練の安定性と最終的な画像品質を向上。
  • 方法: 生成器のヤコビ行列 J の大きさに制約をかける。
数式：
$ \mathcal{L}_{pl} = \mathbb{E}_w\mathbb{E}_y (\left\| J^T_w y \right\|_2- a) ^2 $
  • $\mathcal{L}_{pl}$: 正則化項（Regularization Term）。
  • $\mathbb{E}_w$: 中間潜在コード w 上での期待値演算。
  • $\mathbb{E}_y$: RGB画像空間上のランダム単位ベクトル y 上での期待値演算。
  • $J_w$: 生成器のヤコビ行列（Jacobian Matrix）。中間潜在コード w 。
  • $J^\top_w$: ヤコビ行列の転置（Transpose）。
  • $y$: RGB画像空間（3×H×W次元）に定義されたランダムな単位ノルムベクトル。
  • $\left| \cdot \right|_2$: L2ノルム（ユークリッドノルム）。
  • $a$: 目標となる勾配スケール（通常 a=1）。

利点: 隠れ空間の逆転（invertibility）が容易になり、画像の属性解析や編集が可能になる。

惰性正則化（Lazy Regularization）

  • 主損失関数とは別に、一定間隔で正則化項のみを更新。
  • 例：主損失関数を 16 回更新した後に 1 回だけ正則化項を更新。
効果：
  • 訓練の安定性向上
  • 計算コストの削減
  • Adam オプティマイザの内部状態を共有することで、学習効率を最適化

渐進的成長（Progressive Growing）の見直し

題点

  • 各解像度が一時的に最終出力となるため、高周波成分の過剰学習が起こる。
  • 翻訳不変性の喪失（例：頭部の動きに合わせて歯の位置が追従しない）

新しい代替設計（非漸進的）

名称 概要 特徴
MSG-GAN スキップ接続で複数解像度を融合 mipmap 出力を生成し、多段階表示に対応
Input/output skips 上/下サンプリング時にスキップ接続 各解像度のRGB出力を統合
Residual nets 残差接続を使用 LAPGAN に似るが、各解像度の判別器は不要

StyleGAN v3

  • StyleGAN2 における「テクスチャが画面上に固定されてしまう」問題を根本的に解決。
  • 生成された画像の細部（髪の毛、目、口など）が、対象物の位置・角度に応じて自然に移動するようにする。

問題の具体例：

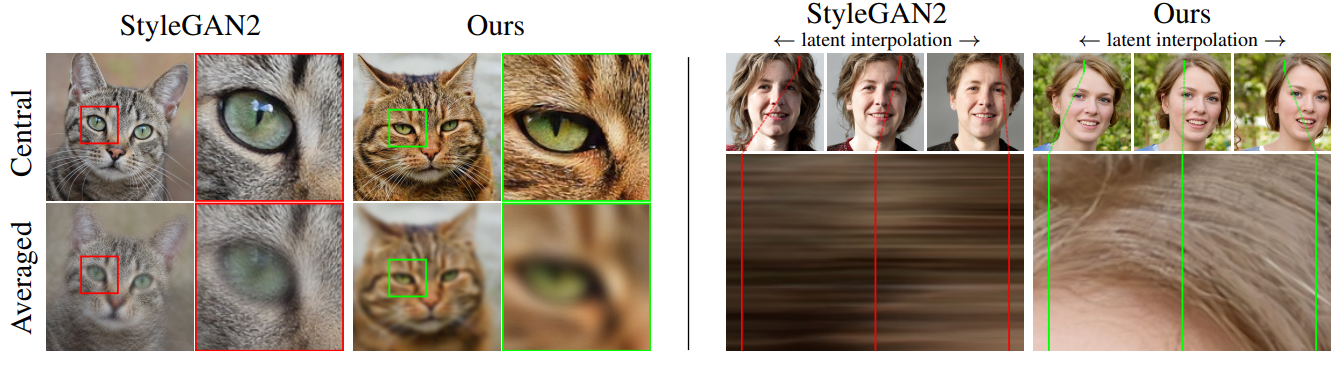
stylegan2v3

  • StyleGAN2 では、顔を横にずらしても、髪の毛やほくろなどの特徴が画面座標系に固定されてしまい、現実的な移動に追随しない。
  • これは GAN 全般に見られる問題で、浅層ネットワークの出力が深層ネットワークの空間位置を十分に制御できていないことを意味します。

StyleGAN2 の限界

  • 畳み込み + 非線形活性化 + アップサンプリングの組み合わせは、平移や回転に対して等変性を持たない。
  • 以下の要素が問題の主因とされています：
要素 問題点
padding / boundary処理 特徴マップの端を明確にするために使われるが、これが画像境界の情報をリークさせ、座標依存性を生む
ノイズ入力 ランダム性を与えるために必要だが、それが局所的なピクセル位置に強く依存してしまう
非線形活性化関数 ReLU や Swish は高周波成分を増幅し、エイリアシング（aliasing）によるグリッド状の歪みを引き起こす

信号処理理論に基づく再設計

StyleGAN3 では、畳み込みネットワークの各操作を「連続信号のサンプリング」として再定義し、等変性を理論的に保証する設計を行っています。

基盤となる生成器構造の変更

  • Fourier 特徴への置き換え:定数入力ではなく、空間的位置情報を持つ周波数ベースの初期特徴を使用
  • ノイズ入力の削除: 位置情報は前の層から受け継ぐべき → ノイズは不要
  • ネットワーク深度の縮小（18層→14層）: 過剰な非線形を減らし、信号の流れを滑らかに
  • Mixing Regularization / Path Length Regularization の無効化 : これらの正則化が等変性を妨げる可能性があるため
  • 畳み込み前での簡単な正規化導入: 数値安定性と勾配の収束を改善

バウンダリ拡張と理想的なアップサンプリング

  • 特徴マップのバウンダリ拡張: 理論上、特徴マップは無限空間を持つが、実装上は有限領域を使う。それを少し広げ、各層で crop を行うことで近似。
  • 双線形アップサンプリングの置き換え: sinc フィルタ + Kaiser窓を用いた理想低域フィルタに変更。
    Kaiser窓は過渡帯域と減衰特性を調整可能。
  • 平移等変性は向上したが、FID スコアは悪化 → 後述の改良が必要

非線形活性化の最適化

  • LReLU をカスタムCUDAカーネルに統合: アップサンプリングとダウンサンプリングとの間に入れることで、aliasing 抑制を強化
  • Pointwise 非線形の aliasing 対策: 高周波成分の漏れを防ぐために、低域フィルタリングを導入

エイリアシング（Aliasing）の抑制

  • エイリアシング高周波成分が低周波として誤って表現される現象。GAN ではこれが座標に固定されたグリッド状の歪みを引き起こす。
  • 対策: 浅い層では高周波成分を意図的に除去（重要度が低い）、深い層では維持することでバランスを取る。
  • 追加のトリック: このような工夫により FID スコアも StyleGAN2 より改善

全体的な空間変換能力の獲得

  • フーリエ特徴へのアフィン変換の導入:学習可能なアフィン変換層を追加し、全体の平移・回転パラメータを w から推定
  • 効果:FID の改善 + 空間変換の柔軟性向上

平移等変性のさらなる強化（T改版）

内容 説明
レイヤー正規化の新設計 局所的な平均・分散を正規化し、空間的変化に対する一貫性を向上
フィルターの再設計 最低解像度層では高い減衰率を設定し、最高解像度層では微細構造を維持

回転等変性の実現（R改版）

内容 説明
3×3 畳み込みを 1×1 に置き換え 空間的な偏りをなくし、ローカルな相関を排除
特徴マップ数を倍に拡大 容量の低下を補完
sinc → jinc フィルタへ変更 径向対称性を持たせることで、回転等変性を強化

等変性の定義

$ g(t[z_0]; w) = t[g(z_0; w)] $
  • $g$: 生成器
  • $z_0$: 初期特徴（Fourier 特徴）
  • $w$: スタイルコード
  • $t$: 平移や回転などの変換

この等式は、「初期特徴に変換 $t$ を適用してから生成器に入れた場合」と「生成器の出力に変換 $t$ を適用した場合」が一致することを示しています。つまり、生成器自体が変換に対して不変な挙動をすることが保証されます。

アーキテクチャの変化

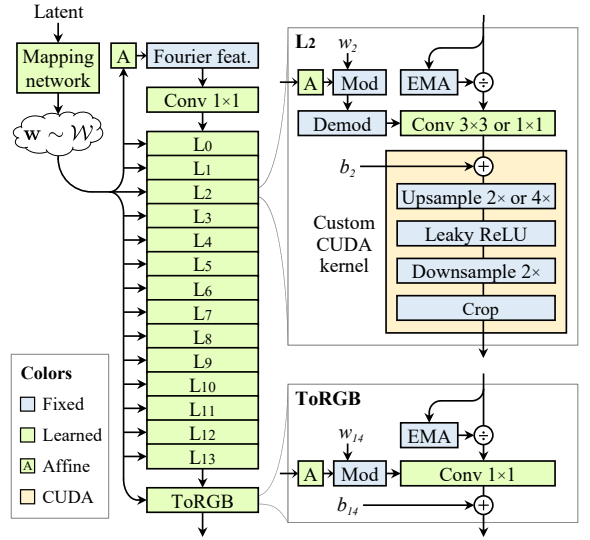
stylegan v3

操作 StyleGAN2 StyleGAN3
初期入力 定数テンソル Fourier 特徴
ノイズブランチ 使用 削除
畳み込みカーネル 通常 3×3 1×1 畳み込み（R版）
アップサンプリング 双線形 sinc / jinc フィルタ + Kaiser窓
非線形活性化 LReLU カスタムCUDA内核で aliasing 抑制
正規化 AdaIN → Modulation/Demodulation LayerNorm などを追加

参考資料

avatar
lijunjie2232
個人技術ブログ
記事
18
タグ
19
カテゴリ
3
My Github
目次0