時系列予測基礎：RNN、LSTM、GRU

目次

• 目次
• リカレントニューラルネットワーク (RNN)
  • 隠れ状態を持たないニューラルネットワーク
  • 隠れ状態を持つRNN
  • 出力層
  • 特徴
  • RNNをもちいる言語モデル
    • RNNによる予測プロセス
• RNNの限界
  • 長期依存関係の学習困難
    • 具体例
  • 計算の逐次性
  • 固定長の隠れ状態
  • 学習の不安定性
• LSTM
  • 核心コンセプト
    • 勾配消失問題への対処
  • 三重のゲート (gate) 構造
  • LSTMのゲート計算の数式
  • 入力ノード (input node)
  • メモリセル状態 (memory cell state)
  • 隠れ状態 (hidden state)
  • コード例
• GRU
  • ゲート (gate) の簡略化
    • 数式的表現
  • 候補隠れ状態（Candidate Hidden State）
    • 数式的表現
    • 動作の直感的理解
  • 隠れ状態（Hidden State）
    • 最終的な隠れ状態の計算
    • 動作の直感的理解
  • コード例
• 参考文献

---

リカレントニューラルネットワーク (RNN)

リカレントニューラルネットワーク（RNN）は、隠れ状態（hidden state）を持つニューラルネットワークです。この隠れ状態により、ネットワークは時系列データの履歴情報を保持し、現在の出力を計算することができます。

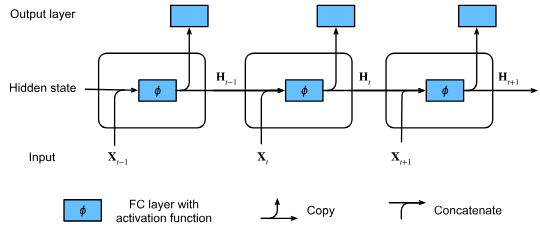
隠れ状態を持たないニューラルネットワーク

まず、隠れ状態を持たない多層パーセプトロン（MLP）を考えてみましょう。入力 $\mathbf{X}$ に対して、隠れ層の出力 $\mathbf{H}$ は次のように計算されます。

$$
\mathbf{H} = \phi(\mathbf{X} \mathbf{W}{\textrm{xh}} + \mathbf{b}\textrm{h})
$$

ここで、$\phi$ は活性化関数、$\mathbf{W}{\textrm{xh}}$ は重み、$\mathbf{b}\textrm{h}$ はバイアスです。

隠れ状態を持つRNN

RNNでは、隠れ層の出力 $\mathbf{H}_t$ は現在の入力 $\mathbf{X}t$ だけでなく、1つ前の時刻の隠れ状態 $\mathbf{H}{t-1}$ にも依存します。

$$
\mathbf{H}t = \phi(\mathbf{X}t \mathbf{W}{\textrm{xh}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hh}} + \mathbf{b}\textrm{h})
$$

この式により、RNNは時系列の履歴情報を保持し、現在の出力を計算することができます。隠れ状態 $\mathbf{H}_t$ は、時系列の現在の「状態」または「記憶」として機能します。

出力層

RNNの出力層は、通常のMLPと同様に計算されます。

$$
\mathbf{O}t = \mathbf{H}t \mathbf{W}{\textrm{hq}} + \mathbf{b}\textrm{q}
$$

特徴

• 時系列情報の保持: RNNは隠れ状態を通じて、過去の入力情報を持つことができます。
• パラメータ数の固定: 時刻が増加しても、RNNのパラメータ数は増加しません。同じパラメータが各時刻で再利用されます。
• 言語モデルへの応用: RNNは、文字レベルや単語レベルの言語モデルを構築するために使用されます。

RNNをもちいる言語モデル

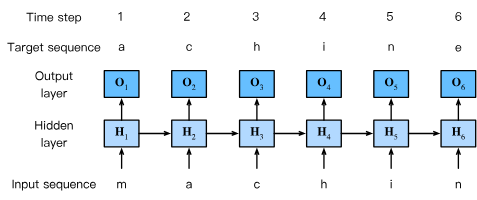
言語モデルの目的は、現在および過去のトークン（単語や文字）に基づいて、次のトークンを予測することです。RNNを用いた文字レベル言語モデルでは、テキストを文字単位でトークン化し、1文字ずつ予測していきます。

例えば、“machine"という単語のシーケンスを考えると、入力シーケンスは"machin”、ターゲットシーケンスは"achine"となります。各時刻tにおいて、RNNは過去の文字列に基づいて次の文字を予測します。

RNNによる予測プロセス

RNNは各時刻tにおいて、以下の手順で処理を行います：

1. 現在の入力文字 $\mathbf{X}t$ と前の隠れ状態 $\mathbf{H}_{t-1}$ から新しい隠れ状態 $\mathbf{H}_t$ を計算
2. 隠れ状態 $\mathbf{H}_t$ から出力 $\mathbf{O}_t$ を生成
3. 出力に対してsoftmax関数を適用し、各文字の出現確率を算出
4. クロスエントロピー損失を用いて、予測結果と正解ラベル（次の文字）との誤差を計算
5. 例えば、時刻3では、入力シーケンス「m」「a」「c」に基づいて出力 $\mathbf{O}_3$ が生成され、正解の文字「h」と比較して損失が計算されます。

RNNの限界

長期依存関係の学習困難

RNNは理論上、任意の長さの時系列情報を保持できますが、実際には勾配消失のため、数百〜数千ステップ前の情報は効果的に学習できません。

具体例

例えば、言語モデルで以下の文を考えます：
“フランスの首都は…パリです。”

「パリ」を予測するには「フランスの首都は」という文脈が必要ですが、RNNは長い文脈の場合、この関係性を学習するのが困難です。

計算の逐次性

RNNの更新は逐次的に行われるため、並列化が難しく、学習や推論が遅くなります。

$$
h_t = f(h_{t-1}, x_t)
$$

この式からわかるように、時刻tの計算は時刻$t-1$の結果に依存するため、並列処理ができません。

固定長の隠れ状態

RNNの隠れ状態$h_t$は固定長のベクトルであるため、時系列が長くなるにつれて情報を圧縮する必要があります。これは情報の損失を引き起こします。

学習の不安定性

• 初期値に敏感
• ハイパーパラメータの調整が難しい
• 学習率の選択が重要で、適切でないと学習が進まない

LSTM

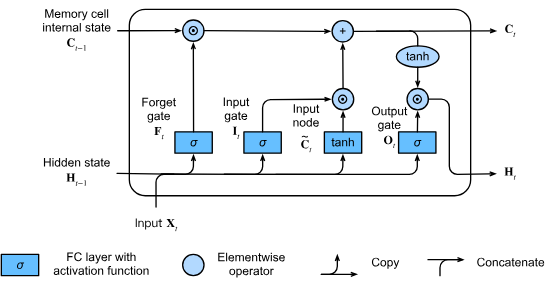
従来のRNNでは、勾配消失・爆発問題により長期依存関係を学習するのが困難でした。LSTM(Hochreiter & Schmidhuber, 1997)はこの問題を解決するため、以下のような革新的な構造を導入しました

核心コンセプト

• メモリセル：時系列情報を保持する中間記憶領域
• ゲート機構：情報の流入・流出を制御する3つの多重ノード
• 定数誤差フロー：勾配が消失/爆発しない設計

勾配消失問題への対処

1. 定数誤差ループ：$\frac{\partial C_t}{\partial C_{t-1}} = F_t \in (0,1) $ を満たすような関数 $f(x)$ を定義により、勾配が指数関数的に減衰しない
2. 多重ノード構造：各ゲートが独立して学習されるため、複雑な依存関係をモデル化可能
3. 非線形活性化の分離：tanhとsigmoid関数が異なる役割を分担し、数値安定性を確保

三重のゲート (gate) 構造

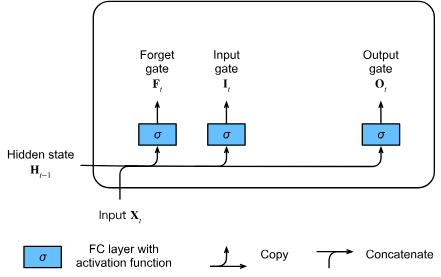
1. 入力ゲート ($\mathbf{I}_t$): 新しい情報がセル状態にどれだけ影響を与えるかを制御
2. 忘却ゲート ($\mathbf{F}_t$): 以前のセル状態の情報をどれだけ保持するかを制御
3. 出力ゲート ($\mathbf{O}_t$): 現在のセル状態が隠れ状態にどれだけ影響を与えるかを制御

ゲート	機能
入力ゲート(input gate)	新しい情報の流入許可
忘却ゲート(forget gate)	古い情報の保持/破棄
出力ゲート(output gate)	セル状態の出力制御

LSTMのゲート計算の数式

数学的に、$h$ 個の隠れユニット、バッチサイズ $n$、入力数 $d$ があると仮定します。したがって、入力は $\mathbf{X}t \in \mathbb{R}^{n \times d}$ で、前の時間ステップの隠れ状態は $\mathbf{H}{t-1} \in \mathbb{R}^{n \times h}$ です。これに対応して、時間ステップ $t$ におけるゲートは次のように定義されます：入力ゲートは $\mathbf{I}_t \in \mathbb{R}^{n \times h}$、忘却ゲートは $\mathbf{F}_t \in \mathbb{R}^{n \times h}$、出力ゲートは $\mathbf{O}_t \in \mathbb{R}^{n \times h}$ です。これらは次のように計算されます：

$$
\begin{aligned}
\mathbf{I}t &= \sigma(\mathbf{X}t \mathbf{W}{\textrm{xi}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hi}} + \mathbf{b}\textrm{i})\
\mathbf{F}t &= \sigma(\mathbf{X}t \mathbf{W}{\textrm{xf}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hf}} + \mathbf{b}\textrm{f})\
\mathbf{O}t &= \sigma(\mathbf{X}t \mathbf{W}{\textrm{xo}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{ho}} + \mathbf{b}\textrm{o})
\end{aligned}
$$

ここで、$\mathbf{W}{\textrm{xi}}, \mathbf{W}{\textrm{xf}}, \mathbf{W}{\textrm{xo}} \in \mathbb{R}^{d \times h}$ および $\mathbf{W}{\textrm{hi}}, \mathbf{W}{\textrm{hf}}, \mathbf{W}{\textrm{ho}} \in \mathbb{R}^{h \times h}$ は重みパラメータで、$\mathbf{b}\textrm{i}, \mathbf{b}\textrm{f}, \mathbf{b}_\textrm{o} \in \mathbb{R}^{1 \times h}$ はバイアスパラメータです。合計中にブロードキャストがトリガーされることに注意してください。入力値を区間 $(0, 1)$ にマッピングするためにシグモイド関数を使用します。

各成分の意味を以下に示します：

• $\mathbf{X}_t$: 時間ステップ $t$ における入力ベクトル（バッチサイズ $n$、入力次元 $d$）
• $\mathbf{H}_{t-1}$: 時間ステップ $t-1$ における隠れ状態（バッチサイズ $n$、隠れユニット数 $h$）
• $\mathbf{W}{\textrm{xi}}, \mathbf{W}{\textrm{xf}}, \mathbf{W}_{\textrm{xo}}$: 入力から各ゲートへの重み行列（入力次元 $d$ × 隠れユニット数 $h$）
• $\mathbf{W}{\textrm{hi}}, \mathbf{W}{\textrm{hf}}, \mathbf{W}_{\textrm{ho}}$: 前の隠れ状態から各ゲートへの重み行列（隠れユニット数 $h$ × 隠れユニット数 $h$）
• $\mathbf{b}\textrm{i}, \mathbf{b}\textrm{f}, \mathbf{b}_\textrm{o}$: 各ゲートのバイアス項（1 × 隠れユニット数 $h$）
• $\sigma$: シグモイド活性化関数（出力を0から1の間に制限）

入力ノード (input node)

$$
\tilde{\mathbf{C}}t = \textrm{tanh}(\mathbf{X}t \mathbf{W}{\textrm{xc}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hc}} + \mathbf{b}\textrm{c})
$$

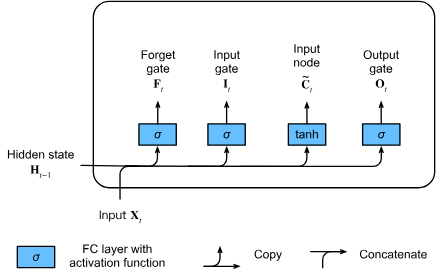
• セル状態に追加される候補情報を生成
• tanh活性化関数で[-1,1]の範囲に正規化

メモリセル状態 (memory cell state)

$$
\mathbf{C}_t = \mathbf{F}t \odot \mathbf{C}{t-1} + \mathbf{I}_t \odot \tilde{\mathbf{C}}_t
$$

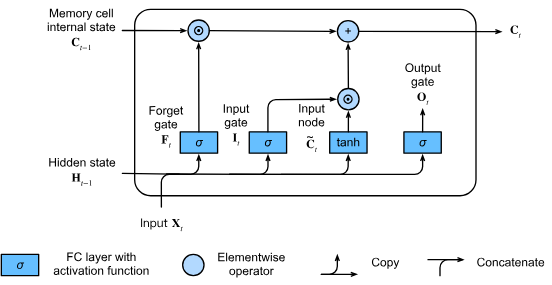
• Hadamard積(要素ごとの積)で情報の更新を制御
• 忘却ゲートが1の時、過去の情報が維持される

隠れ状態 (hidden state)

$$
\mathbf{H}_t = \mathbf{O}_t \odot \tanh(\mathbf{C}_t)
$$

• 出力ゲートでフィルタリングされた情報を出力
• tanhで活性化されたセル状態が最終出力に反映される

コード例

import torch.nn as nn
import torch.nn.functional as F

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(LSTM, self).__init__()
        self.hidden_size = hidden_size
        self.i2h = nn.Linear(input_size, 4 * hidden_size)
        self.h2h = nn.Linear(hidden_size, 4 * hidden_size)
        self.i2h_bn = nn.BatchNorm1d(4 * hidden_size)
        self.h2h_bn = nn.BatchNorm1d(4 * hidden_size)
        self.cx_bn = nn.BatchNorm1d(hidden_size)

    def forward(self, input, cell):
        hx, cx = cell
        input = self.i2h_bn(self.i2h(input)) + self.h2h_bn(self.h2h(hx))
        gates = F.sigmoid(input[:, :3*self.hidden_size])
        in_gate = gates[:, :self.hidden_size]
        forget_gate = gates[:, self.hidden_size:2*self.hidden_size]
        out_gate = gates[:, 2*self.hidden_size:3*self.hidden_size]
        input = F.tanh(input[:, 3*self.hidden_size:4*self.hidden_size])
        cx = (forget_gate * cx) + (in_gate * input)
        hx = out_gate * F.tanh(self.cx_bn(cx))
        return hx, cx

GRU

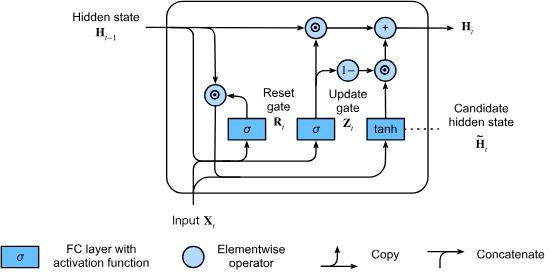
GRU（Gated Recurrent Unit）は、2010年代にRNN、特にLSTM（Long Short-Term Memory）アーキテクチャが急速に普及した時期に開発されました。LSTMは内部状態と乗法的ゲート機構を組み合わせることで、従来のRNNが抱えていた勾配消失問題を解決し、長期依存関係を学習できるようになりました。

しかし、LSTMは入力ゲート、忘却ゲート、出力ゲートの3つのゲートを持つ複雑な構造のため、計算コストが高く、学習や推論に時間がかかるという問題がありました。このため、研究者たちはLSTMの核心的な概念（内部状態とゲート機構）を維持しながら、よりシンプルで計算効率の良いアーキテクチャを模索し始めました。特に、LSTMの記憶セル状態と隠れ状態を統合し、ゲートの数を減らしたことで、パラメータ数が削減され、計算グラフが単純化されたため、勾配の流れがよりスムーズになり、学習が安定するという利点もあります。

ゲート (gate) の簡略化

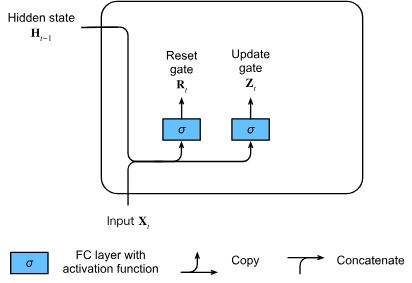
LSTMでは3つのゲート（入力ゲート、忘却ゲート、出力ゲート）を使用していましたが、GRUではこれらを2つのゲートに簡略化しています。それがリセットゲート（reset gate）と更新ゲート（update gate）です。

LSTMと同様に、これらのゲートにはシグモイド活性化関数が適用され、出力値は0から1の間に制限されます。これは、各ゲートが「どの程度情報を通すか」を確率的に表現するためです。

直感的に理解すると：

• リセットゲート：前の時刻の隠れ状態（情報）をどの程度記憶し続けるかを制御します
• 更新ゲート：新しい状態が古い状態の単純なコピーであることをどの程度許容するかを制御します

数式的表現

時刻$t$における入力がミニバッチ$\mathbf{X}t \in \mathbb{R}^{n \times d}$（サンプル数$n$、入力次元数$d$）で、前の時刻の隠れ状態が$\mathbf{H}{t-1} \in \mathbb{R}^{n \times h}$（隠れユニット数$h$）であるとします。

このとき、リセットゲート$\mathbf{R}_t$と更新ゲート$\mathbf{Z}_t$は以下のように計算されます：

$$
\begin{aligned}
\mathbf{R}t = \sigma(\mathbf{X}t \mathbf{W}{\textrm{xr}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hr}} + \mathbf{b}\textrm{r}),\
\mathbf{Z}t = \sigma(\mathbf{X}t \mathbf{W}{\textrm{xz}} + \mathbf{H}{t-1} \mathbf{W}{\textrm{hz}} + \mathbf{b}\textrm{z}),
\end{aligned}
$$

ここで：

• $\mathbf{W}{\textrm{xr}}, \mathbf{W}{\textrm{xz}} \in \mathbb{R}^{d \times h}$ は入力から各ゲートへの重み行列
• $\mathbf{W}{\textrm{hr}}, \mathbf{W}{\textrm{hz}} \in \mathbb{R}^{h \times h}$ は前の隠れ状態から各ゲートへの重み行列
• $\mathbf{b}\textrm{r}, \mathbf{b}\textrm{z} \in \mathbb{R}^{1 \times h}$ は各ゲートのバイアス項
• $\sigma$ はシグモイド関数

この構造により、GRUはLSTMと比較してパラメータ数を削減しながらも、同様のゲート制御メカニズムを維持しています。

候補隠れ状態（Candidate Hidden State）

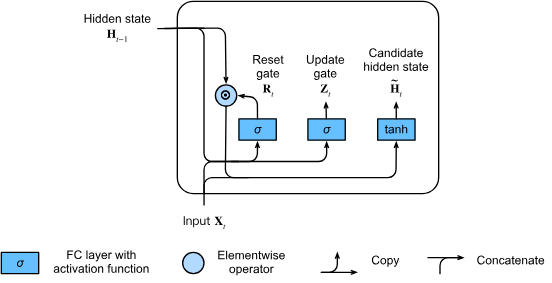
次に、リセットゲート$\mathbf{R}_t$を通常のRNN更新メカニズムと統合することで、時刻$t$における候補隠れ状態（candidate hidden state）$\tilde{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$を計算します。

数式的表現

候補隠れ状態は以下の式で表されます：

$$
\tilde{\mathbf{H}}t = \tanh(\mathbf{X}t \mathbf{W}{\textrm{xh}} + \left(\mathbf{R}t \odot \mathbf{H}{t-1}\right) \mathbf{W}{\textrm{hh}} + \mathbf{b}_\textrm{h})
$$

ここで：

• $\mathbf{W}{\textrm{xh}} \in \mathbb{R}^{d \times h}$ と $\mathbf{W}{\textrm{hh}} \in \mathbb{R}^{h \times h}$ は重みパラメータ
• $\mathbf{b}_\textrm{h} \in \mathbb{R}^{1 \times h}$ はバイアス項
• $\odot$ はアダマール積（要素ごとの積）を表す演算子
• $\tanh$ は双曲線正接活性化関数

動作の直感的理解

この計算結果は「候補」隠れ状態と呼ばれるのは、更新ゲートの作用をまだ組み込んでいないからです。

通常のRNNと比較して、GRUではリセットゲート$\mathbf{R}t$と前の隠れ状態$\mathbf{H}{t-1}$の要素ごとの乗算を用いることで、前の状態の影響を減らすことができます。

• リセットゲート$\mathbf{R}_t$の要素が1に近い場合：通常のRNNと同等になります
• リセットゲート$\mathbf{R}_t$の要素が0に近い場合：候補隠れ状態は$\mathbf{X}_t$を入力とする多層パーセプトロン（MLP）の結果となり、既存の隠れ状態はデフォルト値に「リセット」されます

隠れ状態（Hidden State）

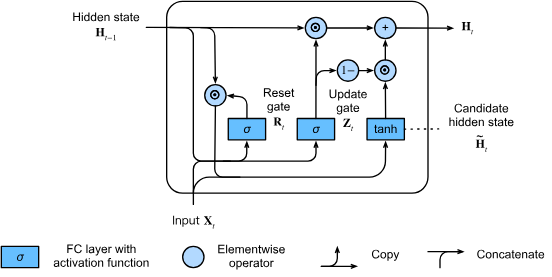
最後に、更新ゲート$\mathbf{Z}_t$の効果を組み込む必要があります。これにより、新しい隠れ状態$\mathbf{H}t$が古い状態$\mathbf{H}{t-1}$にどの程度一致するか、そして新しい候補状態$\tilde{\mathbf{H}}_t$にどの程度似ているかが決定されます。

最終的な隠れ状態の計算

更新ゲート$\mathbf{Z}t$を用いることで、$\mathbf{H}{t-1}$と$\tilde{\mathbf{H}}_t$の要素ごとの凸結合（convex combinations）を取ることで、最終的な隠れ状態を計算します：

$$
\mathbf{H}_t = \mathbf{Z}t \odot \mathbf{H}{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t
$$

この式の動作を理解するために：

• $\mathbf{Z}t \odot \mathbf{H}{t-1}$：更新ゲートの値に応じて古い状態をどれだけ保持するか
• $(1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t$：更新ゲートの値に応じて新しい候補状態をどれだけ採用するか

動作の直感的理解

更新ゲート$\mathbf{Z}_t$の値によって、GRUの動作は大きく異なります：

1. 更新ゲート$\mathbf{Z}_t$が1に近い場合：

   • 古い状態$\mathbf{H}_{t-1}$をほぼそのまま保持
   • 時刻$t$の入力情報$\mathbf{X}_t$は無視され、依存関係の連鎖において時刻$t$が事実上スキップされる

2. 更新ゲート$\mathbf{Z}_t$が0に近い場合：

   • 新しい隠れ状態$\mathbf{H}_t$は候補隠れ状態$\tilde{\mathbf{H}}_t$に近づく
   • 新しい情報が積極的に採用される

コード例

import torch
import torch.nn as nn

class GRU(nn.Module):
    def __init__(self, hidden_size, item_num, state_size, gru_layers=1):
        super(GRU, self).__init__()
        self.hidden_size = hidden_size
        self.item_num = item_num
        self.state_size = state_size
        self.item_embeddings = nn.Embedding(
            num_embeddings=item_num + 1,
            embedding_dim=self.hidden_size,
        )
        nn.init.normal_(self.item_embeddings.weight, 0, 0.01)
        self.gru = nn.GRU(
            input_size=self.hidden_size,
            hidden_size=self.hidden_size,
            num_layers=gru_layers,
            batch_first=True
        )
        self.s_fc = nn.Linear(self.hidden_size, self.item_num)

    def forward(self, states, len_states):
        # Supervised Head
        emb = self.item_embeddings(states)
        emb_packed = nn.utils.rnn.pack_padded_sequence(emb, len_states, batch_first=True, enforce_sorted=False)
        emb_packed, hidden = self.gru(emb_packed)
        hidden = hidden.view(-1, hidden.shape[2])
        supervised_output = self.s_fc(hidden)
        return supervised_output

    def forward_eval(self, states, len_states):
        # Supervised Head
        emb = self.item_embeddings(states)
        emb_packed = nn.utils.rnn.pack_padded_sequence(emb, len_states, batch_first=True, enforce_sorted=False)
        emb_packed, hidden = self.gru(emb_packed)
        hidden = hidden.view(-1, hidden.shape[2])
        supervised_output = self.s_fc(hidden)

        return supervised_output

参考文献

1. d2l
2. Recurrent Neural Networks (RNNs): A gentle Introduction and Overview
3. Long Short-Term Memory
4. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling