AutoEncoder、DAE と VAE (VAE実装含む)

2024/4/6 AI Deep Learning PyTorch Python 機械学習 AI 人工知能深層学習生成AI 画像生成画像処理画像生成AI 自動エンコーダー可変自動エンコーダー

オートエンコーダー（Autoencoder）

オートエンコーダーは、主に教師なし学習に使われるニューラルネットワークの一種で、データの効率的な表現を学ぶことを目的とします。特に、次元削減や特徴抽出に用いられます。

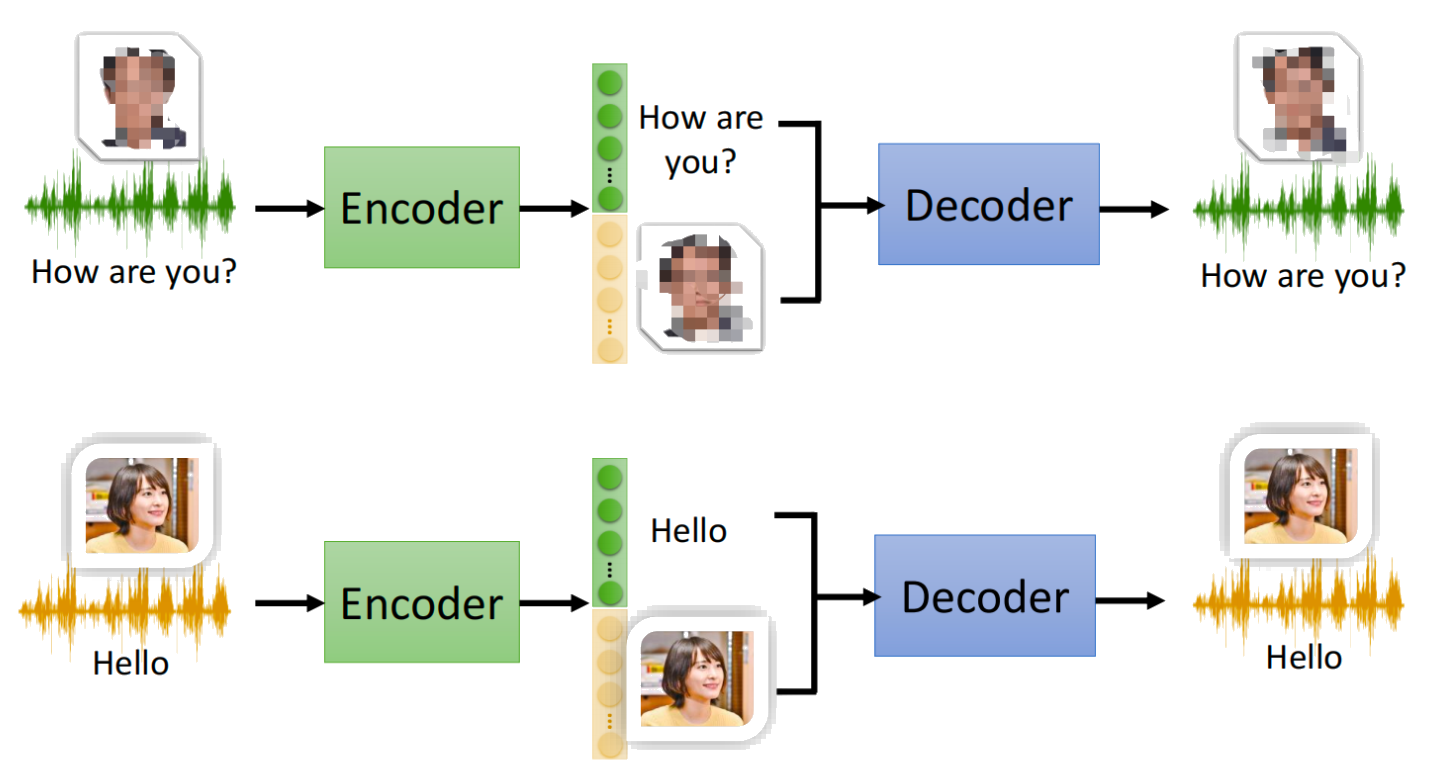
Autoencoder

エンコーダー（Encoder）：入力データを低次元空間に圧縮。
潜在ベクトル（Bottleneck/Code）：圧縮された情報が格納される部分。
デコーダー（Decoder）：潜在ベクトルから元の入力データを復元。

数式による表現

入力データ：$ x $
再構成されたデータ：$ x’ $
潜在空間での表現（圧縮された特徴）：$ z $

エンコード関数（Encoder）：

$$
z = f(x)
$$

$ f(x) $ はニューラルネットワークで構成される関数であり、入力 $ x $ を低次元の潜在変数 $ z $ に変換します。

デコード関数（Decoder）：

$$
x’ = g(z)
$$

$ g(z) $ もニューラルネットワークで構成され、潜在変数 $ z $ から入力 $ x $ と似たデータを再構成します。

目的関数（損失関数）：

AE の目的は、出力 $ x’ $ が入力 $ x $ にできるだけ近づくように学習することです。一般的には次のような損失関数を使用します：

MSE（平均二乗誤差）：

$$
\mathcal{L} = |x - x’|^2_2
$$

Binary Cross Entropy（バイナリ交差エントロピー）：
画像が0〜1の範囲の値を持つ場合などに使用されます。

応用例

次元削減（PCAの非線形版）
ノイズ除去（Denoising AE）
異常検知（再構成誤差が大きい＝異常）
特徴抽出（潜在空間 $ z $ を他のタスクに利用）

コード例

import torch
import torch.nn as nn

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64)
        )
        self.decoder = nn.Sequential(
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784)
        )

    def forward(self, x):
        z = self.encoder(x)
        return self.decoder(z)

DAE(Denoising Autoencode)

DAE（Denoising Autoencoder）は、ノイズ除去を目的としたオートエンコーダー（Autoencoder）の一種です。通常のオートエンコーダーとは異なり、意図的にノイズを加えた入力データから、ノイズを取り除いた元のデータを再構成するように学習します。

DAE

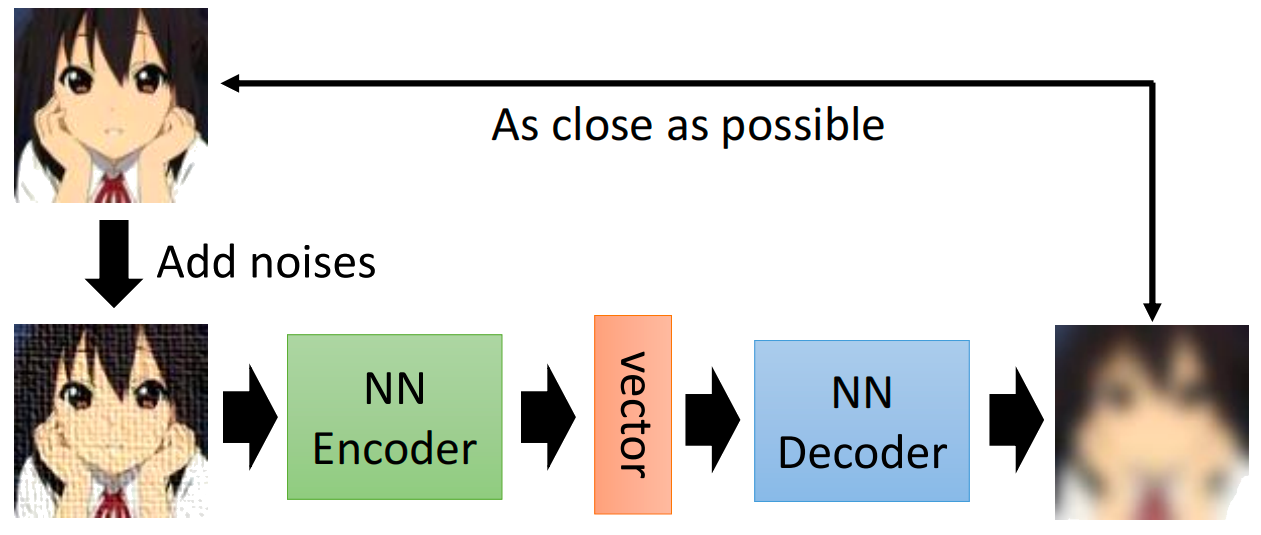
基本的な仕組み

入力にノイズを加える
入力データ $ x $ に対して、ある種のノイズ（例：ガウシアンノイズ、マスクノイズ）を加えて、損なわれたデータ $ \tilde{x} $ を作ります。
エンコーダーで潜在表現を抽出
損なわれたデータ $ \tilde{x} $ をエンコーダー関数 $ f $ に入力し、潜在ベクトル $ z $ を得ます：
$$
z = f(\tilde{x})
$$
デコーダーで元のデータを再構成
潜在ベクトル $ z $ をデコーダー関数 $ g $ を使って復元し、元のノイズなしデータ $ x $ に近づける：
$$
\hat{x} = g(z)
$$
損失関数で誤差を最小化
再構成された $ \hat{x} $ とオリジナルの $ x $ の間の誤差（MSEやBCEなど）を最小化することで、モデルがノイズを除去できるように学習させます。

数式による表現

ノイズ入り入力：
$$
\tilde{x} = x + \epsilon, \quad \text{where } \epsilon \sim \mathcal{N}(0, \sigma^2)
$$
エンコード：
$$
z = f(\tilde{x})
$$
デコード：
$$
\hat{x} = g(z)
$$
損失関数(MSE)：
$$
\mathcal{L} = |x - \hat{x}|_2^2
$$

実装例

import torch
import torch.nn as nn
import torch.nn.functional as F

class DenoisingAutoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU()
        )
        self.decoder = nn.Sequential(
            nn.Linear(256, 784),
            nn.Sigmoid()
        )

    def forward(self, x):
        z = self.encoder(x)
        return self.decoder(z)

# ノイズを加える例（訓練時）
def add_noise(x, noise_factor=0.2):
    return x + noise_factor * torch.randn_like(x)

# 使用例
model = DenoisingAutoencoder()
x_clean = ... # clean image tensor
x_noisy = add_noise(x_clean)
x_recon = model(x_noisy)

loss = F.mse_loss(x_recon, x_clean)  # 損失計算

DAE vs 普通の AE の違い

項目	普通の Autoencoder	Denoising Autoencoder
入力	生データ $ x $	ノイズ付きデータ $ \tilde{x} $
出力	再構成データ $ x’ $	元の生データ $ x $
学習目標	データの圧縮・再構成	ノイズ除去
特徴	潜在空間に構造を捉える	ノイズに頑健な表現を学ぶ

変分オートエンコーダー（Variational Autoencoder, VAE）

VAE とは、対数尤度を最大化するように学習するオートエンコーダーのことです。
新しいデータを生成できるのが大きな特徴です。

VAE

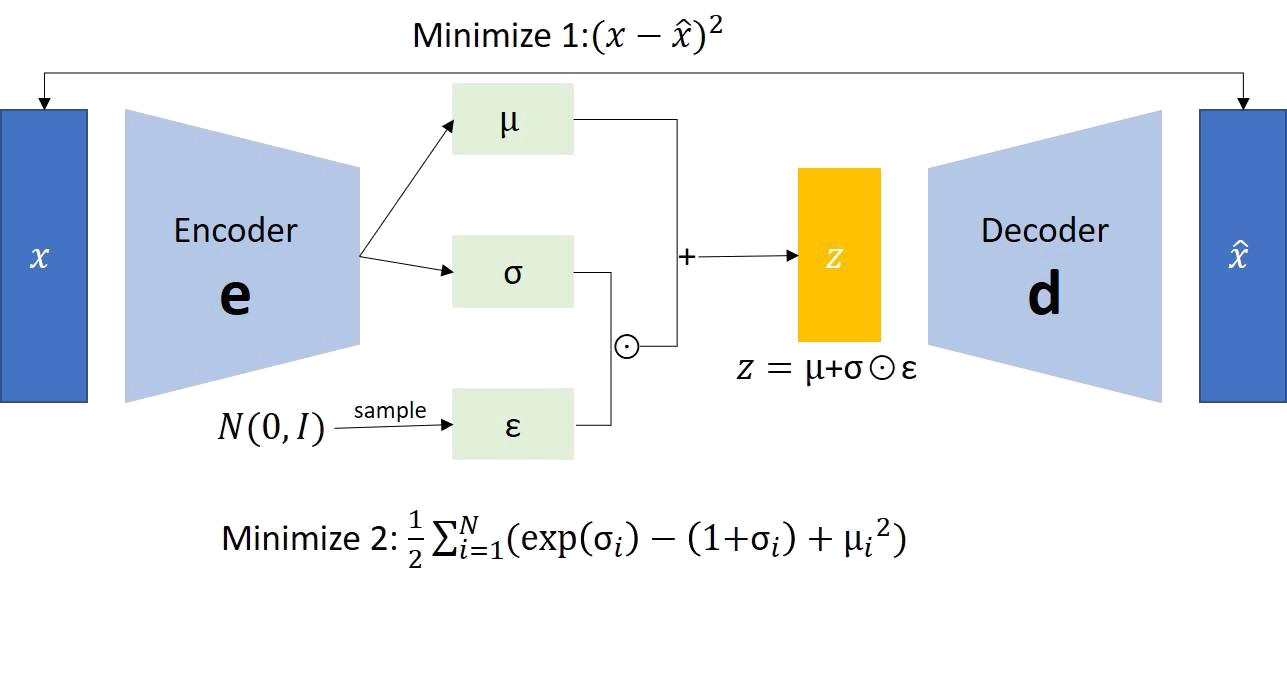
直感的な理解

普通のAutoencoder：入力 $ x $ → 固定値 $ z $ → 再構成 $ x’ $
VAE(Variational Autoencoder)：入力 $ x $ → 正規分布 $ (\mu, \sigma) $ → ノイズ$ \varepsilon \in \mathcal{N}(0,1) $を加え → $ z $ をサンプリング → 再構成 $ x’ $

例：顔画像を入力すると、VAE は「笑顔の強さ」「髪型」「年齢」などの特徴を表す確率分布として潜在空間に表現します。デコーダーはその分布からランダムに値を取り出し、新しい顔画像を生成できます。

VAEの基本構造と原理

VAEは次の2つのネットワークで構成されます：

推論ネットワーク（Encoder）
- 入力 $ x $ を与えると、潜在変数 $ z $ の近似事後分布 $ q(z|x) $ を出力。
- 出力は平均 $ \mu $ と分散 $ \sigma^2 $。
生成ネットワーク（Decoder）
- 潜在変数 $ z $ から入力 $ x $ に類似したデータ $ x’ $ を復元。
- 分布 $ p(x|z) $ をモデル化。

数式による表現

1. Encoder（推論ネットワーク）

$$
q_{\phi}(z|x) = \mathcal{N}(z \mid \mu_{\phi}(x), \sigma_{\phi}^2(x))
$$

平均 $ \mu $ と標準偏差 $ \sigma $ をニューラルネットワークで出力。
潜在変数 $ z $ は以下の方法でサンプリング：
$$
z = \mu + \sigma \cdot \epsilon, \quad \text{where } \epsilon \sim \mathcal{N}(0, 1)
$$
→ この手法は「再パラメータ化トリック」と呼ばれます。

2. Decoder（生成ネットワーク）

$$
p_{\theta}(x|z)
$$

一般的にはベルヌーイ分布（画像など0/1値）やガウシアン分布を使用。
データ $ x $ を $ z $ から復元する条件付き分布。

VAEの目的関数：ELBO（Evidence Lower Bound）

VAEの学習目標は、対数尤度 $ \log p(x) $ を最大化することですが、直接計算は困難です。そのため、ELBO（Evidence Lower Bound） を最大化します。

$$
\log p(x) \geq \mathbb{E}{q(z|x)}[\log p(x|z)] - D{KL}(q(z|x) | p(z))
$$

この右辺が ELBO であり、次のように分解されます：

再構成損失（Reconstruction Loss）
$$
\mathbb{E}_{q(z|x)}[\log p(x|z)]
$$
- デコーダーが出力する $ x’ $ がどれだけ $ x $ に近いかを評価。
- 実装上は BCE（Binary Cross Entropy）や MSE を使用。
KL散逸（KL Divergence）
$$
D_{KL}(q(z|x) | p(z))
$$
- 潜在変数の分布 $ q(z|x) $ が事前分布 $ p(z) $（通常は標準正規分布）に近づくように制約を与える。

VAEの利点・応用

滑らかな潜在空間：隣接する $ z $ 値は似たような出力を生成。
新規データ生成：潜在空間からのサンプリングで新しいデータを生成可能。
内挿・外挿：潜在空間上で線形補間することで、中間的なデータを生成。
応用分野：
- 画像生成（例：顔、風景）
- 音声合成
- 半教師あり学習
- 異常検知（KL項 or 再構成誤差を利用）

実装例

import torch
import torch.nn as nn
import torch.nn.functional as F

class VAE(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)  # mu
        self.fc22 = nn.Linear(400, 20)  # log-variance
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5*logvar)
        eps = torch.randn_like(std)
        return mu + eps*std

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x, reduction='sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE + KLD

AEとVAEの違い

項目	Autoencoder	VAE
学習方法	再構成誤差最小化	ELBO最大化（再構成誤差 + KL散逸）
潜在空間	固定値	確率分布（μ, σ）
データ生成能力	×	◯
応用先	圧縮、ノイズ除去、異常検知	生成モデル、画像生成、潜在空間探索

VAE vs GAN

1. 画像生成のクオリティ

VAE：
- 再構成誤差を最小化するため、全体的な構造は捉えられるが、シャープさに欠ける。
- 出力が「平均的」になりやすく、ぼんやりした画像になりやすい。
GAN：
- 決定論的な判別器とのゲームの中で、非常にリアルでシャープな画像を生成できる。
- 最新のモデル（StyleGAN2, BigGANなど）では人間が見ても区別が難しいレベルまで達している。

2. 学習の安定性

VAE：
- ELBOに基づく明確な目的関数があり、安定して学習が進む。
- 勾配消失などの問題も少なめ。
GAN：
- 生成器と判別器のバランスが難しく、収束しない場合が多い。
- モード崩壊（mode collapse）が発生することもある。

3. 潜在空間の構造

VAE：
- KL散逸によって標準正規分布に近づけられるため、滑らかで連続的な潜在空間を持つ。
- z空間上で線形補間しても自然な変化が得られる。
GAN：
- 潜在空間の構造は必ずしも滑らかではなく、小さなzの変化が急激な出力変化を引き起こすこともある。

4. 理論的背景

VAE：
- 明確なベイズ的枠組み（変分推論）に基づいており、理論的に解析しやすい。
GAN：
- 初期のminimaxゲームとしての理論はあるが、実装依存が強く汎用性が低い。

5. 応用性・拡張性

VAE：
- 半教師あり学習、異常検知、時系列モデリングなどへの拡張が容易。
- β-VAE、CVAE、VAE-GANなど、様々な派生モデルが存在。
GAN：
- 高品質画像生成に特化しており、他タスクへの汎用性はやや劣る。
- StyleGAN, CycleGAN, Pix2Pixなど、特定用途向けに進化。

項目	VAE（Variational Autoencoder）	GAN（Generative Adversarial Network）
目的	確率的潜在空間の学習 + 新規データ生成	高品質なリアルデータの生成
生成画像のクオリティ	中～やや高（ぼんやりしがち）	非常に高い（シャープでリアル）
学習安定性	安定（勾配消失の問題が少ない）	不安定（モード崩壊・収束困難）
潜在空間の滑らかさ	非常に滑らか（補間が自然）	学習により異なる（必ずしも滑らかではない）
理論的裏付け	明確（変分推論 + 確率モデル）	理論的枠組みはあるが実装依存が強い
損失関数の意味	再構成誤差＋KL項（解釈可能）	敵対的なゲーム（損失の意味が曖昧）
サンプリング速度	高速（単純な分布からのサンプリング）	推論ごとに生成器を通す必要あり
多様性（Mode Coverage）	多様性があるが洗練度は低め	モード崩壊のリスクあり（多様性不足）
応用性	特徴抽出、異常検知、内挿にも適する	主に高品位画像生成用途
教師あり学習との併用	可能（半教師ありVAEなど）	制限あり（制約付きGANなどはある）

項目	VAEに向いているケース	GANに向いているケース
用途	特徴抽出、異常検知、潜在空間探索、内挿	高品質画像生成、リアルな画像合成
必要条件	学習の安定性、理論的保証	高品位画像、視覚的インパクト
実装難易度	比較的簡単	難しい（調整が必要）

VAE 実装

環境構築

pip install torch torchvision torchbearer matplotlib numpy

import os
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline  # Jupyter Notebook上でプロットを表示するため

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
from torchvision import transforms
from torchvision.utils import make_grid
from torchvision.datasets import FashionMNIST

import torchbearer
import torchbearer.callbacks as callbacks
from torchbearer import Trial, state_key

データの前処理

transform = transforms.Compose([transforms.ToTensor()])  # Tensor型へ変換

# FashionMNISTデータセットをダウンロード
trainset = FashionMNIST(root='../', train=True, transform=transform)
testset = FashionMNIST(root='../', train=False, transform=transform)

# DataLoaderでミニバッチを生成
traingen = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=8)
testgen = torch.utils.data.DataLoader(testset, batch_size=128, shuffle=False, num_workers=8)

モデルの構築

MU = state_key('mu')         # 潜在空間の平均値(mu)を保存するキー
LOGVAR = state_key('logvar') # 潜在空間の対数分散(logvar)を保存するキー


class VAE(nn.Module):
    def __init__(self, latent_size):
        super(VAE, self).__init__()
        self.latent_size = latent_size

        self.encoder = nn.Sequential(
            nn.Conv2d(1, 32, 4, 1, 2),   # B,  32, 28, 28
            nn.ReLU(True),
            nn.Conv2d(32, 32, 4, 2, 1),  # B,  32, 14, 14
            nn.ReLU(True),
            nn.Conv2d(32, 64, 4, 2, 1),  # B,  64,  7, 7
        )
        
        self.mu = nn.Linear(64 * 7 * 7, latent_size)
        self.logvar = nn.Linear(64 * 7 * 7, latent_size)
        
        self.upsample = nn.Linear(latent_size, 64 * 7 * 7)
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(64, 32, 4, 2, 1), # B,  64,  14,  14
            nn.ReLU(True),
            nn.ConvTranspose2d(32, 32, 4, 2, 1, 1), # B,  32, 28, 28
            nn.ReLU(True),
            nn.ConvTranspose2d(32, 1, 4, 1, 2)   # B, 1, 28, 28
        )

    def reparameterize(self, mu, logvar):
        if self.training:
            std = torch.exp(0.5*logvar)
            eps = torch.randn_like(std)
            return eps.mul(std).add_(mu)
        else:
            return mu

    def forward(self, x, state):
        image = x
        x = self.encoder(x).relu().view(x.size(0), -1)
        
        mu = self.mu(x)
        logvar = self.logvar(x)
        sample = self.reparameterize(mu, logvar)
        
        result = self.decoder(self.upsample(sample).relu().view(-1, 64, 7, 7))
        
        if state is not None:
            state[torchbearer.Y_TRUE] = image
            state[MU] = mu
            state[LOGVAR] = logvar
        
        return result

入力画像をエンコーダー→潜在変数→デコーダーで再構成。
state に中間結果を保存して損失計算などに利用。

損失関数の定義

β倍のKL項を加えることで潜在空間の学習を制御（β-VAEのような挙動）。

def beta_kl(mu_key, logvar_key, beta=5):
    @callbacks.add_to_loss
    def callback(state):
        mu = state[mu_key]
        logvar = state[logvar_key]
        return -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) * beta
    return callback

visualization

学習中に再構成画像を定期的に表示して進捗を確認。

def plot_progress(key=torchbearer.Y_PRED, num_images=100, nrow=10):
    @callbacks.on_step_validation
    @callbacks.once_per_epoch
    def callback(state):
        images = state[key]
        image = make_grid(images[:num_images], nrow=nrow, normalize=True)[0, :, :]
        plt.imshow(image.detach().cpu().numpy(), cmap="gray")
        plt.show()
    
    return callback

モデルの学習

model = VAE(latent_size=10)
optimizer = optim.Adam(filter(lambda p: p.requires_grad, model.parameters()), lr=5e-4)
trial = Trial(model, optimizer, nn.MSELoss(reduction='sum'), metrics=['acc', 'loss'], callbacks=[
    beta_kl(MU, LOGVAR),
    callbacks.ConsolePrinter(),
    plot_progress()
], verbose=1).with_generators(train_generator=traingen, test_generator=testgen)
trial.to('cuda')     # GPU使用設定
trial.run(20)        # 20エポック学習
trial.evaluate(verbose=0, data_key=torchbearer.TEST_DATA)

MSE Loss：再構成誤差を最小化。
beta_kl：KL項を追加。
plot_progress：毎エポックごとに画像を表示。
ConsolePrinter：ログ出力。
trial.to(‘cuda’)：GPUでの高速処理を有効化。

結果のビジュアライゼーション

VAE data

LOADING

AutoEncoder、DAE と VAE (VAE実装含む)

目次

オートエンコーダー（Autoencoder）

数式による表現

エンコード関数（Encoder）：

デコード関数（Decoder）：

目的関数（損失関数）：

応用例

コード例

DAE(Denoising Autoencode)

基本的な仕組み

数式による表現

実装例

DAE vs 普通の AE の違い

変分オートエンコーダー（Variational Autoencoder, VAE）

直感的な理解

VAEの基本構造と原理

数式による表現

1. Encoder（推論ネットワーク）

2. Decoder（生成ネットワーク）

VAEの目的関数：ELBO（Evidence Lower Bound）

VAEの利点・応用

実装例

AEとVAEの違い

VAE vs GAN

1. 画像生成のクオリティ

2. 学習の安定性

3. 潜在空間の構造

4. 理論的背景

5. 応用性・拡張性

VAE 実装

環境構築

データの前処理

モデルの構築

損失関数の定義

visualization

モデルの学習

結果のビジュアライゼーション